Доколку имате искуство со решавање на задачи преку пишување на програми, тогаш веќе се имате запознаено со повеќе податочни структури, алгоритми, термини и задачи од областа на теоријата на графови, итн. Секако, и во предавањата кои се дадени на овој систем, користевме голем број на податочни структури и алгоритми - особено тие што се веќе имплементирани во програмскиот јазик C++ (queue, vector, итн).

Во продолжение, ќе се запознаеме со една податочна структура која се користи многу често, особено за време на натпревари по информатика. Истата служи за ефикасно извршување на операции врз опсег од елементи во една низа – на пример, проблеми од типот “колку е збирот на сите елементи во низата почнувајќи од 3-тиот до 10-тиот”, “промени ја вредноста на 7-миот по ред елемент во низата”, итн.

Пред да продолжиме понатаму, да размислиме како примерите што ги споменавме погоре можеме да ги решиме со користење на низа, и извршување на едноставни алгоритми врз таа низа. На пример, нека имаме низа од N елементи, и нека индексите на елементите во таа низа почнуваат од 0, па се до N-1 (како што работевме со низи и досега). Сега, доколку имаме задача каде што треба да извршуваме разни операции од типот: “пресметај го збирот на сите елементи со индекс помеѓу X и Y”, или “пресметај го производот на сите елементи со индекс помеѓу X и Y”, потребно е да напишеме for циклус кој ќе ги измине сите индекси од X, X+1, X+2, ..., Y-1, Y, притоа одржувајќи една променлива која ќе го памети потребниот збир или производ – како што е прикажано подолу.

int sum(int x, int y) 
{
     int total = 0;
     for (int i=x; i <= y; i++) 
     {
          total += array[i];
     }
     
     return total;
}

Очигледно, овој алгоритам има линеарна временска сложеност O(N), бидејќи е неопходно да ги поминеме сите потребни елементи од низата по еднаш, со цел збирот/производот да ја содржи точната вредност.

Од друга страна пак, доколку сакаме да ажурираме некој елемент од низата (array[i] = V), тоа можеме да го направиме во константно време O(1), бидејќи е потребно да ја промениме вредноста на само еден елемент во низата.

Со помош на сегментно дрво (за што ќе зборуваме во продолжение), можеме овие две операции (ажурирање, и пресметка на збир/производ на опсег од соседни елементи) да ги извршуваме со логаритамска временска сложеност O(logN). (Покрај збир и производ, оваа структура може да се користи и за решавање на други слични проблеми, за што ќе зборуваме подолу во предавањето).

Иако едноставниот алгоритам кој го разгледавме претходно е ефикасен при промената на вредности (во константно време), фактот што операциите за разгледување на опсег од вредности се вршат во линеарно време го прави непрактичен во ситуации кога е потребно да се извршуваат голем број на операции од тој тип. На пример, доколку имаме низа од 1 000 000 елементи и одлучиме да користиме сегментно дрво, секоја операција за пресметка на збир или производ на опсег од соседни елементи ќе се врши со разгледување на само log(N) елементи, односно на околу 20 вредности од податочната структура.

Имплементација

На наша жалост, сегментно дрво не е имплементирано во Стандардната Библиотека на Шаблони (STL), па ќе мораме да го имплементираме самите – на пример, за време на натпревар по информатика. Иако за да го напишеме истото не е потребно многу време или многу код - сепак, во продолжение, ќе поминеме доста време на објаснување зошто оваа податочна структура функционира толку ефикасно, а ќе споменеме и кои се работите на кои треба да внимавате за време на имплементација на истата. Ова ќе го направиме поради фактот што сегментно дрво е навистина важна податочна структура, која може да се применува за решавање на разни проблеми и задачи.

Најпрвин, да видиме како функционира истото. Нека имаме низа array[], во која имаме запишано N цели броеви. Сегментно дрво не е ништо повеќе од дополнителна низа tree[], во која што елементите на одредени позиции содржат одговори на оригиналниот проблем за опсези од почетната низа. На пример, ако користиме низа со име tree[] за имплементација на сегментно дрво (како што споменавме погоре), и истото го користиме за брзи пресметки на збир во одреден опсег, во tree[1] ќе го чуваме збирот на сите броеви од оригиналната низа array[0] до array[N-1], во tree[2] ќе го чуваме збирот на половина од броевите во оригиналната низа (од array[0] до array[N/2]), итн… Имајќи вакви вредности, можеме брзо да пресметуваме одговори на оригиналниот проблем, бидејќи сега нема потреба да ги поминуваме сите елементи од една низа за пресметка на потребниот збир. Како пример, доколку не користевме сегментно дрво и сакавме да пресметаме колку е збирот на сите елементи со индекс од 0 до N-1, ќе требаше да ги поминеме сите тие N вредности, а доколку користиме сегментно дрво, доволно е само да погледнеме што е запишано во tree[1]. Доколку сакаме да промениме некоја вредност, потребно е да се променат само O(logN) вредности во сегментното дрво, за истото да може да врши пресметки врз разни опсези. Оваа идеја е прикажана на следната слика.

Забележете како tree[1] го чува збирот на сите елементи од A[0] до A[9], како tree[2] го чува збирот на сите елементи од A[0] до A[4], итн. Постојат 10 делови од кои нема понатамошно делење, каде што сите чуваат по само една вредност од оригиналната низа – ова му овозможува на сегментното дрво да дава одговори дури и кога, на пример, одреден опсег содржи само 1 елемент.

Операциите за ажурирање и пресметка на потребната вредност за некој опсег ќе ги имплементираме со помош на рекурзија. Како пример за сликата дадена погоре, да кажеме дека сакаме да го пресметаме збирот на сите елементи со индекси од 0 до 7. Во овој случај, рекурзијата ќе започне од првиот (најгорниот) елемент во дрвото, и истата ќе забележи дека таму се содржи збирот на сите елементи со индекси од 0 до 9. Нажалост, бидејќи нас не интересира збирот (само) на елементите од 0 до 7, вредноста запишана таму не можеме да ја искористиме, па рекурзивно ќе прејдеме на следниот ред. Во левата страна (tree[2]) имаме збир на елементите со индекси од 0 до 4, а бидејќи нас не интересира целиот збир од 0 до 7, нема веќе потреба да продолжиме рекурзивно надолу, бидејќи можеме да ја земеме таа вредност (tree[2]) и да забележиме дека веќе сме завршиле со пресметка на збирот на елементи од 0 до 4. Бидејќи рекурзивно продолживме и на десната страна (tree[3]), таму ќе мораме да прејдеме и во третиот ред, поради фактот што во tree[3] е запишан збирот на елементите со индекси од 5 до 9, а нас воопшто не не интересираат елементите со индекс 8 и 9, и не сакаме нивната вредност да е дел од збирот. Кога ќе прејдеме во третиот ред, во tree[6] е содржан збирот на елементите со индекси од 5 до 7, па вредноста запишана таму можеме да ја собереме со вредноста запишана во tree[2], со што ќе го имаме збирот на сите елементи од 0 до 7 – бидејќи во tree[2] е збирот на елементите со индекси од 0 до 4, а во tree[6] и збирот на оние со индекс од 5 до 7.

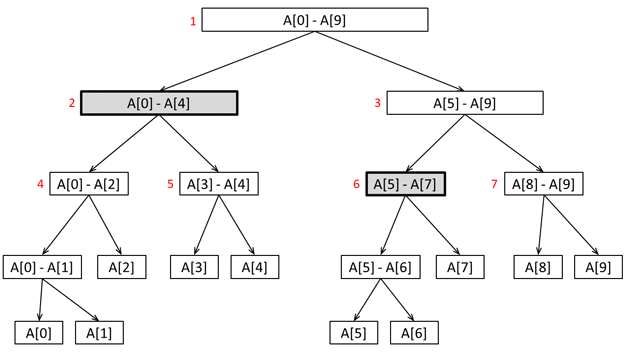
Како што можете да забележите, главната цел е пресметка на вредност за опсег од елементи, без разгледување (поединечно) на сите тие елементи – т.е., користејќи подсуми.

Во продолжение, ќе видиме како можеме да имплементираме сегментно дрво во програмскиот јазик C++. Во функцијата main(), за да нема потреба да внесуваме низи и голем број на елементи, ќе користиме rand() за создавање на низа со случајно генерирани вредности. Слично, наместо да внесуваме неколку опсези преку стандарден влез, ќе користиме rand() за создавање на нивниот лев и десен индекс (на пример, 3 и 7 за пресметка на збирот на вредности во низата почнувајќи од 3 до 7, итн). Ова го правиме чисто информативно. Се разбира, нема потреба од користење на rand() или било кои други (слични) функции за време на решавање на вистински проблеми. Едноставно, главната функција main() ја користиме со единствена цел за да покажеме како се извршуваат операции врз сегментно дрво.

Втората (и многу поважна) работа која што треба да ја споменеме е дека функциите за ажурирање на вредност update() и за пресметка на збир на елементи во некој опсег query(), ќе прифаќаат по 5 вредности како параметри – 2 логични, но и 3 дополнителни за рекурзијата да знае кој елемент од сегментното дрво се разгледува во даден момент. На пример, во query(from, to, interval_index, interval_left, interval_right), со from и to означуваме дека сакаме истата да го пресмета збирот на сите елементи со индекси од from до to; но имаме и три дополнителни вредности, каде што со interval_index означуваме кој индекс од сегментното дрво го разгледуваме во моментот (на пример, 1 доколку го разгледуваме tree[1] – каде што е запишан збирот на сите елементи од оригиналната низа, итн), а со interval_left и interval_right е означен опсегот кој што е запишан во тој елемент од сегментното дрво (на пример, interval_left=0, interval_right=N-1, доколку го разгледуваме елементот tree[1], бидејќи таму е запишан збирот на сите елементи од 0 до N-1). Понатаму, како што ќе се движиме низ рекурзијата, истата ќе ги менува овие вредности (interval_index=2, interval_index=3, итн).

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;

const int MAX_5N = 500001;
int tree[MAX_5N];

void update(int pos, int value, int interval_index, int interval_left, int interval_right) 
{
     //momentno gledame vo tree[interval_index],
     //shto go sodrzhi intervalot [interval_left...interval_right]
     
     if (interval_left > pos || interval_right < pos || interval_left > interval_right) 
     {
          //intervalot e celosno levo ili desno od pozicijata (pos) koja sakame da ja azurirame
          return ;
     }
     
     if (interval_left == interval_right) 
     {
          //dojdovme do poslednoto nivo vo drvoto, pa azuriraj ja vrednosta
          if (interval_left == pos) 
          {
               tree[interval_index] = value;
          }
          
          return ;
     }
     
     //inaku, rekurzivno azuriraj ja levata i desnata polovina od intervalot
     int middle = (interval_left + interval_right) / 2;
     update(pos, value, (2 * interval_index), interval_left, middle);
     update(pos, value, (2 * interval_index + 1), middle+1, interval_right);
     
     //od koga kje zavrshime so rekurzijata, zbirot kaj sekoe teme e zbir od negovite deca
     tree[interval_index] = (tree[2 * interval_index] + tree[2 * interval_index + 1]);
}

int query(int from, int to, int interval_index, int interval_left, int interval_right) 
{
     //momentno gledame vo tree[interval_index],
     //shto go sodrzhi intervalot [interval_left...interval_right]
     
     if (interval_left > to || interval_right < from || interval_left > interval_right) 
     {
          //intervalot e celosno levo ili desno od opsegot za koj sakame da presmetame suma
          return 0;
     }
     
     if (from <= interval_left && interval_right <= to) 
     {
          //intervalot e celosno vo opsegot za koj sakame da presmetame suma, pa dodadi go
          return tree[interval_index];
     }
     
     int middle = (interval_left + interval_right) / 2;
     
     int sum_left = query(from, to, (2 * interval_index), interval_left, middle);
     int sum_right = query(from, to, (2 * interval_index + 1), middle+1, interval_right);
     
     return (sum_left + sum_right);
}




int main() 
{
     
     int n = 1000;
     memset(tree, 0, sizeof(tree));
     
     for (int i=0; i<1500; i++) 
     {
          
          if (i%2 == 0) 
          {
               
               //napravi azuriranje na vrednosta kaj "indeks"
               int index = rand() % n;
               int value = rand() % 79103;
               
               update(index, value, 1, 0, n-1);
          }
          else 
          {
               
               //presmetaj ja sumata na posledovatelni vrednosti
               int number1 = rand() % n;
               int number2 = rand() % n;
               
               int from = min(number1, number2);
               int to = max(number1, number2);
               
               int sum = query(from, to, 1, 0, n-1);
               cout << "sum of elements in the interval [" << from << "," << to << "] is: " << sum << endl;
          }
     }
     
     return 0;
}

Најпрвин, забележете дека функциите update() и query() се доста слични една на друга, што ја прави оваа структура практична за имплементација. Секоја од функциите, најпрвин ги разгледува параметрите за да провери дали интервалот од сегментното дрво кој што се разгледува во тој момент е можеби целосно надвор од она што ни е потребно. На пример, во update(), доколку сакаме да ажурираме вредност кај индексот pos=3, а интервалот е од interval_left=5 до interval_left=6, тогаш можеме веднаш да ја прекинеме рекурзијата. Ова е многу важно да се направи, доколку сакаме функцијата да има временска сложеност O(logN). На крајот од првиот if услов, јас обично сакам да ја додадам и проверката (interval_left > interval_right), која што иако не може да се случи доколку правилно ја имплементираме функцијата, сепак го прави условот покомплетен – едноставно, доколку интервалот е погрешен (не може левиот крај да е поголем од десниот), тогаш можеме веднаш да прекинеме со разгледување на истиот.

Понатаму, во следниот чекор, во функцијата update() проверуваме дали сме стигнале до интервал кој содржи само еден елемент, и доколку индексот на тој елемент е оној индекс кој сакаме да го ажурираме, ја правиме промената. Во функцијата query(), од друга страна, проверуваме дали интервалот кој го разгледуваме целосно се содржи во опсегот за кој го бараме збирот (на пример, интервалот е [0, 4], а бараме збир на елементите со индекси од 0 до 7). Во тој случај, нема потреба да продолжиме натаму со рекурзијата, бидејќи не треба да го делиме интервалот на два помали делови кога ни е потребен збирот на целиот тој интервал.

Во спротивно, на крајот од функциите, го делиме интервалот на два дела. Индексот (interval_index) во двата помали делови е точно 2*interval_index (за левиот дел) и 2*interval_index + 1 (за десниот дел). На пример, доколку моментно го разгледуваме елементот tree[1] од сегментното дрво, двата делови под него се оние со tree[2*1] и tree[2*1 + 1]. Од кога рекурзивно ќе ја направиме пресметката за двата помали делови, пристигаме до клучниот и најважниот елемент од алгоритамот. Имено, да започнеме со разгледување од функцијата update(). Од кога рекурзивно ќе се направи пресметка за двата помали интервали, ја имаме линијата

tree[interval_index] = (tree[2 * interval_index] + tree[2 * interval_index + 1])

Со наредбата, запишуваме дека збирот во големиот интервал во кој што сега се наоѓаме е еднаков на збирот од вредностите запишани во помалите интервали. Ова ни овозможува, во функцијата query(), да не мора да се движиме и да ги разгледуваме сите елементи, бидејќи сега знаеме дека секој елемент tree[x] ја содржи точната вредност, и доколку се ажурирал некој помал интервал под него, со таа линија сме ја ажурирале и вредноста на tree[x]. Слично, во функцијата query(), на крајот имаме (sum_left + sum_right); па доколку збирот зависи и од делови кои се наоѓаат во левата, и од делови кои се наоѓаат во десната половина, тогаш конечниот збир ќе ги содржи сите нив.

Забележете дека во овој проблем пресметувавме збир на елементи во одреден опсег; но, со сегментно дрво можат да се решат и други проблеми – пресметка на производ (множење), НЗД (најголем заеднички делител) на елементи од даден опсег, и други проблеми каде што важи комутативниот закон. Притоа, ќе треба да направите само мали промени на функциите. На пример, за множење, можеме само да ја промениме операцијата од собирање (+) во множење (*), односно (sum_left + sum_right) во (sum_left * sum_right), и (tree[2 * interval_index] + tree[2 * interval_index + 1]) во (tree[2 * interval_index] * tree[2 * interval_index + 1]). Дополнително, потребно е да направиме промена кај првиот услов во функцијата query(), односно да вратиме 1 наместо 0. Имено, со тој услов проверуваме дали интервалот е целосно надвор од она што не интересира, и доколку е, за множењето сакаме да вратиме вредност 1 (бидејќи понатаму можеме да го помножиме тој број 1 со останатите без да влијаеме на вредноста - бидејќи X*1=X). Доколку множиме со нула, ќе се поништат досега добиените резултати и ќе добиеме вредност 0.

Всушност, правилото кое што треба да го примените за да одлучите дали да користите сегментно дрво е да проверите дали можете да ги искористите вредностите на два помали интервали за да запишете точна вредност во интервалот кој се наоѓа над нив. Кај собирање, ова очигледно важи: збирот на сите елементи од 0 до 9 е еднаков на збирот на (елементите од 0 до 4) и збирот на (елементите од 5 до 9). Слично, истото важи и кај множење, наоѓање на НЗД на опсег од елементи, наоѓање на најмал елемент во опсег, наоѓање на најголем елемент во опсег (најголем елемент во опсегот на елементи од 0 до 9, е еднаков на поголемиот од разгледаните елементи во опсегот од 0 до 4 и опсегот од 5 до 9), итн. За да го искористиме и ова како пример, да споменеме што треба да се промени во програмата за да работиме со наоѓање на најголем елемент во опсег наместо со наоѓање на збир: треба само да направиме промени на (sum_left + sum_right) во max(sum_left, sum_right), и (tree[2 * interval_index] + tree[2 * interval_index + 1]) во max(tree[2 * interval_index], tree[2 * interval_index + 1]). Слично како и со множењето, треба да направиме промена во првиот if услов во функцијата query(), така што сега ќе вратиме некоја многу мала вредност (на пример, -2000000000), која што понатаму нема да влијае на резултатот бидејќи бараме максимум, па другата вредност секогаш ќе биде поголема. Едноставно, нели?

Кај други проблеми, правилото за користење на помалите интервали за ажурирање на интервалот над нив можеби нема да важи: на пример, не важи кај делењето. Ако во едниот интервал во кој се содржат две вредности 4 и 2, сме ја запишале вредноста (4/2 = 2), и ако во другиот интервал се содржат две вредности 9 и 3 па сме ја запишале вредноста (9/3 = 3), како можеме сега во горниот интервал да ги искористиме тие две вредности од интервалите под него (2 и 3), за да пресметаме 4/2/9/3? Едноставно, кај вакви проблеми, не можеме да користиме сегментно дрво.

За крај на овој дел, да споменеме уште една важна информација. Ако ја видиме програмата напишана погоре, ќе забележиме дека имаме создадено низа од 500 001 елементи: tree[500001]. Моја препорака е, кога ќе користите сегментно дрво, да создадете низа со најмалку 5*N елементи (каде N е максималниот број на елементи кои може да ви се најдат во оригиналната низа) - бидејќи, особено денес, компјутерите имаат голема меморија. Ова особено го препорачувам за време на натпревари, за да не изгубите време во пресметки на тоа колку точно елементи треба да има вашето сегментно дрво. На пример, за чување 500 000 елементи ни требаат само 500 000 * 4 бајти, што е помалку од 2 мегабајти меморија. Зошто да не ги искористите истите кога ви е тоа дозволено?

За оние кои што, од теоретски причини, ги интересира колку точно елементи се потребни за сегментното дрво - одговорот е дека, во најлош случај, потребни се 2*S елементи, каде S е првиот поголем или еднаков степен на 2. Степени на 2 се броевите: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, итн. Ако оригиналната низа има N=1000 елементи врз кои сакаме да вршиме операции за ажурирање или пресметки во опсег, тогаш следниот поголем степен на 2 е 1024, па за сегментното дрво ќе требаат 2*S = 2*1024 = 2048 елементи. Едноставно, степенот на 2 доаѓа од фактот што, кај сегментно дрво, во секое следно ниво има два пати повеќе елементи од претходното ниво, а во деловите од кои нема понатамошно делење се наоѓаат интервали од по 1 елемент.

Создавање на дрво

Во претходниот пример, разгледавме сегментно дрво каде што е дозволена промена на вредностите на елементите користејќи го нивниот индекс – и тоа, со логаритамска временска сложеност О(logN). Но, постојат и проблеми каде што вредностите на елементите ќе ни бидат дадени однапред, и тие нема да се менуваат помеѓу извршувањето на наредбите за пресметка на резултатите од даден опсег – т.е. помеѓу повиците на функцијата query(). Кај вакви задачи, доколку вредностите ни се дадени однапред, ќе треба да ја повикаме функцијата update() за секој од тие N елементи, со што временската сложеност за поставување на сите вредности во сегментното дрво би била O(NlogN).

Во ситуации како оваа, можеме да направиме нова функција build(), која што, однапред познавајќи ги вредностите кои треба да се постават за секој индекс, ќе го создаде сегментното дрво во линеарно време O(N). Притоа, бидејќи сегментното дрво ќе функционира на истиот начин како и претходно, нема да има потреба од никакви промени на функцијата query(), а ниту пак на функцијата update(), доколку воопшто и ни треба функција за ажурирање на елементи (на пример, доколку елементите ни се дадени однапред, но ќе треба да се вршат и неколку промени подоцна).

Имплементацијата на функцијата build() е многу слична на функцијата update() што ја видовме претходно - со таа разлика што, кога ќе стигнеме до последното ниво на сегментното дрво (каде што интервалите содржат само по еден елемент), наместо да проверуваме дали индексот одговара на елементот кој сакаме да го промениме, ќе ги промениме вредностите на сите елементи (бидејќи build(), за разлика од update(), треба да ги ажурира сите нив).

//ako imame niza "values", ja povikuvame funkcijata na
//sledniot nachin:   build(values, n, 1, 0, n-1);
void build(int values[], int N, int interval_index, int interval_left, int interval_right) 
{
     //momentno gledame vo tree[interval_index],
     //shto go sodrzhi intervalot [interval_left...interval_right]
     
     if (interval_left < 0 || interval_right >= N || interval_left > interval_right) 
     {
          //proverka dali e se vo red
          return ;
     }
     
     if (interval_left == interval_right) 
     {
          //dojdovme do poslednoto nivo (eden element), azuriraj ja vrednosta
          tree[interval_index] = values[interval_left];
          
          return ;
     }
     
     //rekurzivno odi vo levata i desnata polovina na intervalot
     int middle = (interval_left + interval_right) / 2;
     build(values, N, (2 * interval_index), interval_left, middle);
     build(values, N, (2 * interval_index + 1), middle+1, interval_right);
     
     tree[interval_index] = (tree[2 * interval_index] + tree[2 * interval_index + 1]);
}

Забележете дека, пред повикување на функцијата, треба да ја имаме дефинирано низата values[], која што ги содржи елементите кои треба да ги запишеме во сегментното дрво (values[0] е вредноста на елементот со индекс pos=0, values[1] е вредноста на елементот со индекс pos=1, итн). Како што наведовме, оваа функција треба да се повика само еднаш, кога ќе ги знаеме сите почетни вредности values[], и таа има временска сложеност O(N). Понатаму, можеме да ги користиме функциите update() и query() на ист начин како и претходно.

Дозвола за користење: CC BY-NC 2.5 ©