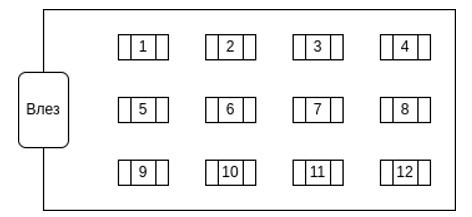
Во една зграда има N станови означени со броевите од 1 до N, на R спратови по C станови. Во подрумот на зградата, секој станар има свое сандаче за писма и пратки, и истите се наредени на земја во форма на R x C матрица, како на долната слика. Броевите на становите растат од лево кон десно во еден ред, и продолжуваат во следниот ред.

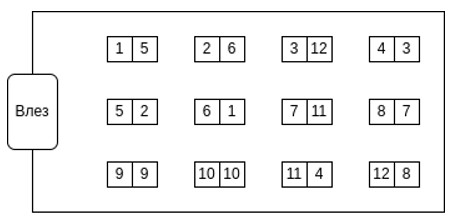
Едно утро поштарот ги донел сметките за струја, ама наместо соодветно да ги распредели, тој во секое сандаче оставил една случајно избрана сметка. Едно можно распоредување на сметките е дадено на долната слика (од лево е бројот на сандачето, а од десно е бројот на станарот за којшто е наменета сметката).

На станарите не им е прв пат да се соочат со овој проблем. Тие знаат и алгоритам како сигурно и побрзо да стигнат до својата сметка: Секој станар прво оди кај сандачето со неговиот број. Откога ќе го отвори, има две можности: или внатре ќе си ја најде својата сметка (и во тој случај ја погледнува сметката, ја остава, и си оди дома), или ќе ја најде сметката на друг станар. Во вториот случај, ја остава туѓата сметка во своето сандаче, и почнува да оди накај сандачето на тој станар. Во тоа сандаче повторно наоѓа сметка, и ако повторно не е неговата, продолжува натаму, на истиот начин, се дури не ја лоцира својата сметка. За да работи стратегијата за сите станари, сметката после видување мора да се остави во сандачето, се дури и последниот станар не ја лоцира својата сметка.

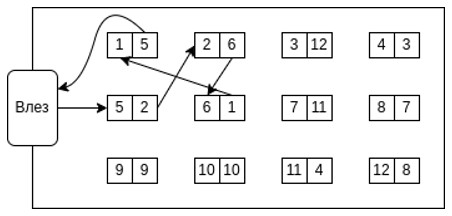
Кога еден станар се наоѓа кај едно сандаче, потребно му е точно една секунда за да стигне до сандачето долу/горе од него, и точно една секунда за да стигне до сандачето лево/десно од него. Станарите не можат да се движат дијагонално, и тие секогаш го следат најкраткиот пат меѓу две сандачиња. На пример, патот на станарот со стан број 5 е даден на долната слика, и вкупното време меѓу сандачињата претставува пет секунди (две секунди од бр. 5 до бр. 2, една секунда од бр. 2 до бр. 6, две секунди од бр. 6 до бр. 1).

Времето од влезот до првото сандаче, и од последното сандаче до излезот, не се бројат. Доколку станарот во своето сандаче веднаш го најде својот број (како станарот со број 9 во примерот), тогаш неговото време е нула секунди.

Ваквото непрофесионално однесување е недозволиво. Затоа секој од станарите го пресметал времето коешто тој го потрошил барајќи го своето писмо. Потоа, вкупното време го пратиле во пошта, со приговор за надомест на штетата.

За даден распоред на сметките во сандачињата, дали би можеле и вие да пресметате колку време им потрошил поштарот на станарите?

Влез

На влез прво се дадени природните броеви R (1 ≤ R ≤ 10 000), број на спратови - редици, и C (1 ≤ C ≤ 10 000), број на станови по спрат - колони. Бројот на станари N е еднаков на R*C.
Потоа следат точно N (1 ≤ N ≤ 1 000 000) броеви M_i,j (1 ≤ M_i,j ≤ N, за 1 ≤ i ≤ R и 1 ≤ j ≤ C) во матрицата M, и тоа секој број ја претставува сметката која се наоѓа во сандачето на соодветниот станар, почнувајќи со сандачето на стан број 1 и одејќи до стан број N. Првиот тест пример ја претставува состојбата дадена во горната слика.

Забелешка. За 27 поени ќе важи: 1 ≤ N ≤ 1 000.

Излез

На излез се бара точно еден број, а тоа е збирот од сите времиња што ги потрошиле станарите.

Ограничувања

Временско ограничување: 200 milliseconds
Мемориско ограничување: 64 megabytes

Примери

влез
3 4
5 6 12 3
2 1 11 7
9 10 4 8

излез
68

Објаснување за примерот:
Станарот бр. 1 ќе потроши 4 секунди. Станарот бр. 2 ќе потроши 4 секунди.

Станарот бр. 3 ќе потроши 9 секунди. Станарот бр. 4 ќе потроши 7 секунди.

Станарот бр. 5 ќе потроши 5 секунди. Станарот бр. 6 ќе потроши 5 секунди.

Станарот бр. 7 ќе потроши 9 секунди. Станарот бр. 8 ќе потроши 9 секунди.

Станарите бр. 9 и бр. 10 нема да потрошат време (точно им е погодено сандачето).

Станарот бр. 11 ќе потроши 9 секунди. Станарот бр 12 ќе потроши 7 секунди.