Нека постои насочен граф G со N темиња (нумерирани од 1 до N) и множество на ребра E. За секој пар темиња a, b во G, 1 < a < b, реброто (a, b) постои во E доколку барем еден од следните услови е исполнет:
1) Вредноста на a е делител на b;
2) Постои теме c (1 < c), така што вредноста на c е делител и на a и на b.

Пример-граф со големина 8 е следниот:

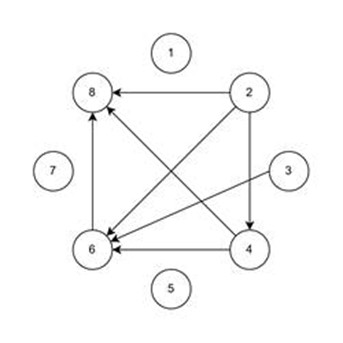Твоја задача е да процесираш Q прашанки на граф со големина N. Постојат два типа на прашанки:
1) За дадено теме V во G, да го вратите влезниот степен на V (вкупниот број на ребра кои што завршуваат, т.е. влегуваат во V);
2) За дадени две темиња L, R во G, L ≤ R, најдете ја сумата на влезните степени за сите темиња во G со вредност во интервалот [L, R] (modulo 10⁹ + 7)

Влез

На влез во првиот ред се наоѓаат три цели броја N (1 ≤ N ≤ 10⁹), Q (1 ≤ Q ≤ 10⁴), и T (типот на прашанки, или 1 или 2).

Потоа, следат Q редови со вредности. Доколку Т = 1, секој ред ќе содржи точно еден цел број V (1 < V ≤ 10⁹). Доколку Т = 2, секој ред ќе содржи пар од цели броеви, L и R ( 1 < L < R ≤ 10⁶).

Подзадачи.
Подзадача 1. (15 поени) T = 1, 1 ≤ N ≤ 10⁴, 1 ≤ Q ≤ 25
Подзадача 2. (25 поени) T = 1
Подзадача 3. (60 поени) T = 2, 1 ≤ N ≤ 10⁶

Излез

За секоја прашанка, во посебен ред да се испечати одговорот.

Ограничувања

Временско ограничување: 200 milliseconds
Мемориско ограничување: 64 megabytes

Примери

влез
8 7 1
2
3
4
5
6
7
8

излез
0
0
1
0
3
0
3

влез
8 2 2
2 8
3 7

излез
7
4

Објаснување на првиот пример: Види ја сликата погоре (пример-графот со големина 8).