Дрвата во програмирањето се структури кои растат од коренот надолу. Коренот е првото теме на дрвото, кое има деца (темиња), кои имаат деца, итн. Коренот е на ниво 0 во дрвото, неговите деца се на ниво 1, децата на неговите деца се на ниво 2, итн. Темињата кои немаат деца се викаат листови. Најголемото ниво кое го има некое теме во дрвото се смета за височина на целото дрво.

Иван е уметник, па ги прашал другарите информатичари како да си одгледа едно програмерско дрво со точно N листа. Тие му го кажале следново:
- Ние ќе ти дадеме едно теме за корен.
- Дрвото расне ниво по ниво. Ти може да одбереш колку деца ќе има секое теме од дадено ниво.
- За секое ниво времето на раснење е различно и ние ќе ти ги кажеме времињата C_i за секое ниво, соодветно. Децата растат едно по едно, па времето за сите деца е производ од C_i и бројот на деца од тоа ниво.
- Вкупниот број на темиња на дадено ниво е исто така ограничен и ние ќе ти ги кажеме ограничувањата P_i за секое ниво, соодветно.

Иван сака да знае, за сите височини од 1 до D, ако најрационално го избира бројот на деца со дадените ограничувања, колку време ќе биде потребно за да го израсне дрвото со соодветната височина.

Помогнете му на Иван и за секој број од 1 до D, утврдете го бараното минимално време на раснење на дрвото, со точно N листови, и со запазени ограничувања P_i.

Влез

Првиот ред се состои од два цели броја: N (1 ≤ N ≤ 10⁶) и D (1 ≤ D ≤ 50 000) – потребниот број на листови во секое од дрвата и најголемата височина, соодветно.

Вториот ред содржи точно D цели броеви C₁, C₂, …, C_D (1 ≤ C_i ≤ 10⁶) – потребното време за да израсне едно теме на ниво i, е C_i.

Третиот ред содржи точно D цели броеви P₁, P₂, …, P_D (1 ≤ P_i ≤ 10⁶) – максималниот број на темиња кои може да израснат на ниво i е P_i.

Забелешка. - За 8% од поените важи: N, D ≤ 10
- За други 12% од поените важи: D ≤ 100, N ≤ 1000
- За други 20% од поените важи: D ≤ 1000, N ≤ 10000
- За други 5% од поените важи: C₁ = C₂ = … = C_D

Излез

Во првиот ред отпечатете D цели броеви, каде i-тиот број е минималното потребно време за Иван да го израсне дрвото со височина i, или -1 доколку не може да се израсне такво дрво.

Ограничувања

Временско ограничување: 100 milliseconds
Мемориско ограничување: 64 megabytes

Примери

влез
3 3
5 3 2
2 3 2

излез
-1 14 15

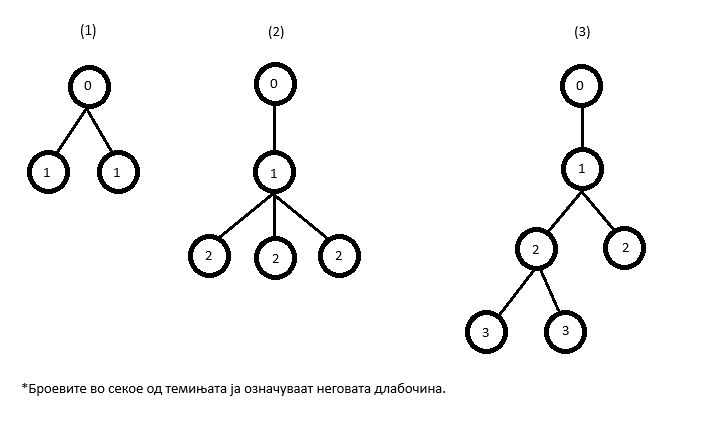Објаснување за примерот:
На ниво 1 може да има најмногу две темиња, па поради тоа што дрвото треба да има N = 3 листа, нема начин како да се израсне првото дрво (одговорот е -1). На ниво два можат да има најмногу 3 темиња, на сликата можеме да видиме една валидна конструкција на дрво со N = 3 листа и височина 2. Второто дрво има едно теме на ниво 1 и три темиња на ниво 2, вкупно 5 * 1 + 3 * 3 = 14. На ниво три може да има најмногу две темиња, на сликата е претставена една валидна конструкција со N = 3 листови и височина 3. Третото дрво има едно теме на ниво 1, две темиња на ниво 2 и две темиња на ниво 3, вкупно 1 * 5 + 2 * 3 + 2 * 2 = 15.