Fuleco the Armadillo is very hungry and, as we all know, his favorite food are ants from a tree. Unfortunately, Fuleco is not a fast animal, so it is not uncommon that ants can escape him by running over tree branches. Ants are also very smart animals and they can smell Fuleco and start running to some other part of a tree which they think is not accessible to Fuleco. In order to help Fuleco the Armadillo not to get tired without a reason, we want to calculate the distance between the starting position of an ant and the position for which the ant thinks it is not accessible to him. And yeah, Fuleco can calculate from this whether he can catch the ant or not.

Let us define the ant-traversal of a tree in the following way. The ant start the traversal from the tree root and walks along the sides of the tree until he returns to the root again. The traversal starts from the left side of the tree. While walking up, the ant always stays on the left side of a branch, and when walking down, the ant is always on the right side of a branch. This traversal can be uniquely represented with a string, defined in the following way. For each visited fork (node) along the path we append letter "U" if the ant goes up from that point, or letter "D" if the ant goes down from that point, until it reaches the next fork (node).

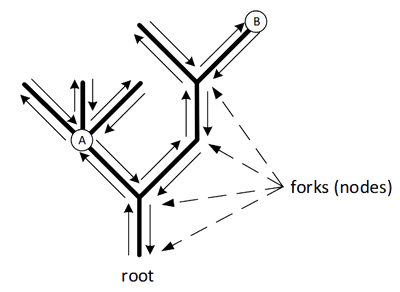Given figure represents example of a tree and ant-traversal is given with directed lines along its side. String representation of this traversal is: UUUDUDUDDUUUDUDDDD.

You are given a string representation of the "ant-traversal" of an unknown tree and two forks (nodes) from that tree. These forks represent the ant's starting position and the position for which the ant thinks it is safe from Fuleco. Forks are specified by its indices in the given string representation, where index k represents the point where the ant will be after walking k times alongside the branches, starting from the root. For example, in the above figure, the fork labeled with "A" can be represented with indices 2, 4, 6 or 8. The distance between nodes "A" and "B" is 4.

Input

The input contains two lines. The first line contains two integers A and B, separated with one space, which are indices of the starting and the final position of the ant. Indices are zero-based. The second line contains one string S which represents the ant-traversal of a tree.

Length of a given string is less than 10⁶. The string represents a valid tree and contains only letters "U" and "D". It will hold 0 <= A, B < length(S). In 50% of test cases it will hold length(S) <= 5 * 10³

Output

The first and only line of the output contains one integer number which is the distance between given nodes in the tree.

Constraints

Time limit: 500 milliseconds
Memory limit: 64 megabytes

Examples

input
4 14
UUUDUDUDDUUUDUDDDD

output
4

This tree is depicted on the figure in the problem statement. The number of branches between given two nodes, i.e. the distance, is 4.