Let’s describe a new “chess” piece and call it "camel-tone". The piece moves jumping: horizontally or vertically – over two chessboard squares, or diagonally – over one square. The picture shows a part of the board with a camel-tone, placed in the center and the positions (marked by x), where it can go with one move. Of course, it cannot go outside the playing board, which happens to be a big square, divided into N×N little squares. In this task N is always divisible by 5.

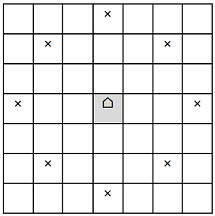The camel-tone starts at the square in the top-left corner of the board. The game consists of making a sequence of moves on the board, visiting every square exactly once. Moreover, after N² -1 moves the piece should be exactly one move away from its starting position. This is a so-called “camel-tonian cycle”!

Write a program camel to find any possible way to play the game, or to report that the cycle is impossible.

Input

A single line is read from the standard input, containing only one integer N (5 <= N <= 1000). N will always be divisible by 5.

Output

The program has to write to the standard output:

- one line with the message NO, if you establish that the cycle is impossible
        or
- N lines, each containing N space separated numbers, which are the different positive integers between 1 and N² inclusive. The first number in the first line is 1. The output represents the playing board (N×N squares), where integers indicate the consecutive occupied positions. See the example below.

Constraints

Time limit: 1 second
Memory limit: 256 megabytes

Examples

input
10

output
1 52 29 8 51 28 9 50 37 16
85 95 59 86 94 66 87 93 65 88
40 19 100 39 18 76 38 17 77 49
2 53 30 7 58 27 10 89 36 15
84 96 60 75 99 67 72 92 64 71
41 20 82 44 23 90 45 24 78 48
3 54 31 6 57 26 11 68 35 14
83 97 61 74 98 62 73 91 63 70
42 21 81 43 22 80 46 25 79 47
4 55 32 5 56 33 12 69 34 13

The camel-tone starts at the top left position (row:1, column:1), numbered 1. The second occupied position is (row:4, column:1), so it is numbered 2. The next position is (row:7, column: 1), and it is numbered 3, and so on. The final (hundredth) occupied position is (row:3, column:3), and it is at one move away from the starting position.
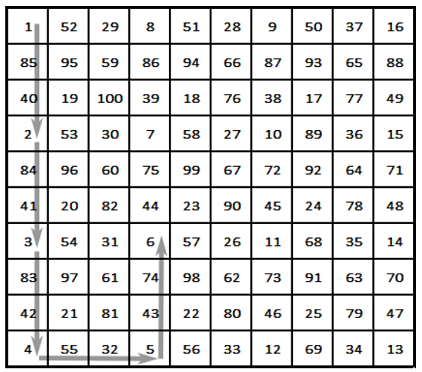