Во една држава постојат N градови означени од 1 до N, и постојат M двонасочни патишта кои поврзуваат по два различни града. Митко ќе оди на патување со својата нова кола на гас, од градот со реден број 1 до градот со реден број N.

Бидејќи новата кола на Митко има мал резервоар, тој ќе мора да надополнува гас во секој од градовите кои ќе ги посетува. Станицата за гас во градот i нуди гас со квалитет V_i. Бидејќи колата на Митко е нова, тој сака да се движи само низ градови каде ќе надополнува гас со висок квалитет. Расположението на Митко можеме да го означиме со R и тоа може да се намали кога полни гас. Кога Митко ќе посети град i со квалитет на гас V_i тогаш неговото расположениe ќе се промени во помалиот број од R и V_i. На почетокот расположението на Митко е V₁ бидејќи ќе наполни гас во градот 1 и тргнува на патување.

Ваша задача е да изберете пат со кој неговото крајно расположение ќе е најголемо можно, а притоа, дополнително, избраниот пат треба да поминува низ најмногу К градови (броејќи ги и градовите 1 и N). Може да бидете сигурни дека постои барем еден пат од градот 1 до градот N кој што поминува низ најмногу K градови. Доколку постојат повеќе патишта со исто крајно расположение тогаш изберете некој кој минува низ најмалку градови.

Од избраниот пат само отпечатете го расположението на Митко после посета на сите градови и бројот на градови кои ќе ги посети.

Влез

Во првиот ред се наоѓаат броевите N ( 1 ≤ N ≤ 100000 ), M ( 1 ≤ M ≤ 200000 ; M ≤ N*(N-1)/2 ) и K ( 1 ≤ K ≤ N ).
Во вториот ред ви се дадени N броеви V₁ V₂ … V_n, каде V_i ( 1 ≤ V_i ≤ 1000000 ) е квалитетот на гасот во градот i.
Во секој од следните M редови дадени се два броеви А_i и B_i ( 1 ≤ A_i, B_i ≤ N; A_i != B_i ) кои означуваат дека постои двонасочен пат помеѓу градовите со редни броеви A_i и B_i.
За најмалку 25% од поените сите V_i се еднакви.

Излез

Во еден ред отпечатете го крајното расположение на Митко и бројот на градови на патот кој ќе го изберете.

Ограничувања

Временско ограничување: 1 second
Мемориско ограничување: 64 megabytes

Примери

влез
8 9 4
10 1 5 5 10 10 10 10
1 2
2 8
1 3
3 4
4 8
1 5
5 6
6 7
7 8

излез
5 4

влез
4 4 3
10 15 5 1
1 2
1 3
2 4
3 4

излез
1 3

Објаснување за првиот тест пример:
Влезот го опишува следниот граф, каде градовите се круговите во кои се испишани нивните индекси а веднаш до нив е испишан и квалитетот на гасот во соодветниот град.

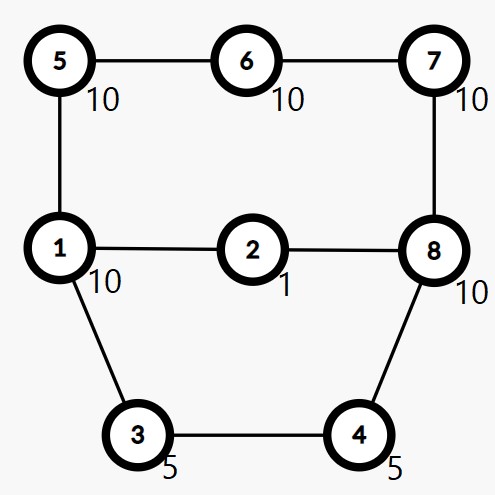Можните движења од почетното теме 1 до крајното теме 8 се следните:

1 – 2 – 8; пат кој поминува низ три градови, расположението во градот 1 е 10, во градот 2 станува 1 и во градот 8 останува на 1.

1 – 3 – 4 – 8; пат кој поминува низ четири градови, расположението во градот 1 е 10, во градот 3 станува 5 и во градовите 4 и 8 останува на 5.

1 – 5 – 6 – 7 – 8; пат кој поминува низ пет градови, расположението во градот 1 е 10 и во градовите 5, 6, 7 и 8 останува на 10.

Можеме да видиме дека најголемо расположение Митко би имал со третиот пат, но тој пат го надминува бројот на градови низ кои смееме да се движиме. Останатите два избори се движат низ дозволениот број на градови 4 или низ помалку градови од тоа, па можеме да избереме било кој. Ќе го избереме оној со повисоко крајно расположение, а тоа е патот 1-3-4-8 со крајно расположение 5.

Објаснување за вториот тест пример:
Иако има избор помеѓу два патишта каде во едниот од нив избегнуваме да се намали расположението во вториот град, сепак крајното расположение секогаш е исто бидејќи последниот град е оној со најнизок квалитет на гас.