Алгоритми. Споредба на алгоритми
Алгоритам претставува конечно множество на чекори (или постапка) за решавање на одреден проблем. На пример, да речеме дека треба да напишеме програма која ќе прочита N (најмногу 1000) цели броеви и ќе го отпечати, на екран, најголемиот прочитан број. Еден алгоритам за решавање на овој проблем би одел вака: прочитај го N, прочитај ги N-те цели броеви во низа, и потоа провери за секој број од низата дали тој број е најголем. Програмата која го имплементира овој алгоритам е дадена во продолжение:
Програма 18.1
#include <iostream>
using namespace std;
int main()
{
int n, p[1000];
cin >> n;
for (int i=0; i<n; i++)
cin >> p[i];
int najgolem = -1;
for (int i=0; i<n; i++)
{
bool eNajgolem = true;
for (int j=0; j<n; j++)
if (p[i] < p[j]) //ima pogolem broj?
eNajgolem = false;
if (eNajgolem)
{
najgolem = p[i];
break;
}
}
cout << najgolem << endl;
return 0;
}
Очигледно, оваа програма го решава зададениот проблем. Но, се поставува прашањето, дали постои некој "поефикасен" алгоритам кој го решава истиот проблем? Притоа, постои постапка (наречена анализа на алгоритми) со која може да се предвиди т.н. временска сложеност на еден алгоритам. Под временска сложеност ќе го подразбираме бројот на операции кои се потребни за да се изврши алгоритамот - за познат број на влезни податоци (на пример, N цели броеви). Притоа, се интересираме за најлошото време на извршување на една програма - ако текот на програмата може да тргне во повеќе насоки, нас не интересира онаа која ќе предизвика програмата да се извршува најдолго.
Основата за предвидување на временската сложеност на еден алгоритам е т.н. "големо О" нотација - на пример, O(N2). Притоа, претпоставуваме дека секоја основна операција се извршува во единечно време. За основни операции ќе ги сметаме сите операции кои се извршуваат во фиксно време - аритметички операции, логички операции, читање и печатење на број, доделување на вредност на променлива, итн. Главната цел на постапката е да открие колку брзо се зголемува времето на извршување на програмата со зголемување на големината на проблемот. При пресметување на временската сложеност, ги елиминираме сите членови на изразот освен најзначајниот, како и сите константи. На пример, за алгоритам кој извршува најмногу 4*N2 + 3*N + 5 операции, велиме дека има временска сложеност O(N2).
Конкретно, O(N) алгоритам ќе работи двојно (2 пати) побавно при двојно зголемување на големината на проблемот - ако за 1000 броеви алгоритамот се извршува 1 секунда, за 2000 броеви алгоритамот ќе се извршува 2 секунди. О(N2) алгоритам ќе работи четири пати побавно при двојно зголемување на големината на проблемот (20002 = 4000000, што е 4 пати поголемо од 10002 = 1000000) - па ако за 1000 броеви алгоритамот се извршува 1 секунда, за 2000 броеви алгоритамот ќе се извршува 4 секунди. Брзината на извршување на алгоритмите кои имааат O(1) временска сложеност не зависи од големината на проблемот - и за 1000 елементи и за 10000 елементи алгоритамот се извршува 1 секунда.
Да го анализираме следниот алгоритам:
Извадок 18.1
int n, zbir = 0; //1 (dodeluvanje na vrednost -> zbir = 0)
cin >> n; //1 (chitanje na podatok)
for (int i=1; i<=n; i++) //2*N+2 -> i=1 (1), i<=n (n+1 pati), i++ (n pati)
zbir += i*i; //2*N -> i*i (n pati), zbir+=... (n pati)
cout << zbir; //1 (pechatenje na podatok)
Вкупното времетраење е (1)+(1)+(2*N+2)+(2*N)+(1) = 4*N + 5
При постапката на предвидување на временската сложеност, со цел да го откриеме времето на извршување на еден алгоритам без да навлегуваме во детали како брзина на процесор, диск, итн, ги занемаруваме сите константи од изразот (4*N + 5*1 » N + 1), бидејќи тие варираат од систем до систем - на пример, замислете една програма да се извршува на два компјутери, каде едниот има 4 пати побрз процесор од другиот. Дополнително, ги занемаруваме сите собироци од изразот освен најзначајниот (N+1 » N). За алгоритамот даден погоре велиме дека има сложеност O(N), или линеарна сложеност. Бидејќи нé интересира времето на извршување на програмата за што поголеми вредности на N, ваквата "апроксимација" е логична и не влијае на корисноста на добиениот резултат - дали една програма ќе изврши N операции или N+1 е ирелевантно за големи вредности на N.
На пример, програма која имплементира алгоритам со сложеност N2+N, за N=10 000 ќе изврши околу 100 000 000 + 10 000 = 100 010 000 операции. Јасно се гледа дека членот N не влијае сериозно на времето на извршување на програмата - 10 000 пати е понезначаен од другиот член (N2) на изразот (при 100 010 000 извршени операции - гледано во бројот од лево на десно, N влијае дури на 5-тата по значајност цифра). За уште поголема вредност на N - на пример N=1 000 000, вториот член во изразот (N) има уште помало влијание - околу 0.0001% од вкупниот број на операции.
Важно е да напоменеме дека, доколку сложеноста зависи од повеќе параметри и немаме некоја информација за тоа како параметрите зависат едни од други или кој параметар доминира во пресметките (на пример, имаме N студенти и M професори и за секој од нив треба да извршиме некоја операција), можно е и изразот да зависи од повеќе променливи, односно да е од типот: O(N+M), О(N*M), или нешто сосема друго.
Бидејќи се интересираме за најлошото време на извршување на програмите, ќе ги користиме следниве правила за пресметка на временската сложеност:
| тек | временска сложеност |
|---|---|
| последователни наредби: A; |
O(A) + O(B) + O(C) |
| условно извршување: if (uslov) |
max{O(A), O(B)} (полошиот случај) |
| циклуси: for (i=1; i<=n; i++) |
n * O(A) ( [колку итерации] * [бр. операции во циклусот] ) |
Од сé што кажавме досега, може да се заклучи дека е едноставно да се открие временската сложеност на една програма преку анализирање на циклусите. Навистина, оној циклус кој е најмногу вгнезден во други циклуси ќе доминира со времето на извршување на програмата (нормално - доколку сите циклуси зависат од ист параметар). Користејќи го ова правило, може да заклучиме дека првата програма која што ја прикажавме има временска сложеност O(N2) - циклусот кој проверува дали тековниот број е најголем ќе доминира при анализата на временската сложеност.
Програма 18.2
#include <iostream>
using namespace std;
int main()
{
int n, p[1000];
cin >> n;
for (int i=0; i<n; i++)
cin >> p[i];
int najgolem = -1;
for (int i=0; i<n; i++)
{
bool eNajgolem = true;
for (int j=0; j<n; j++)
if (p[i] < p[j]) //ima pogolem broj?
eNajgolem = false;
if (eNajgolem)
{
najgolem = p[i];
break;
}
}
cout << najgolem << endl;
return 0;
}
Можеби, во овој момент, се прашувате зошто се интересираме само за најлошиот случај на извршување на програмата и велиме дека временската сложеност е O(N2). Што ако уште првиот елемент е најголем и се изврши наредбата break; - тогаш програмата очигледно нема да изврши N2 операции. Навистина, при некои анализи може да се интересираме за т.н. најдобро време на извршување, или, уште почесто, за просечното време на извршување на една програма. Во просек, програмата дадена погоре ќе измине N/2 цели броеви и за секој од нив ќе провери дали е тоа најголемиот прочитан цел број.
Просечното време на извршување го дефинираме како очекуваниот број на операции кои би се извршиле од страна на еден алгоритам. Ваквото време е многу тешко за проценка и зависи од влезните податоци. Кај некои алгоритми има логика да се испитува просечното време (на пример, алгоритми кои прават случајни одлуки при нивното извршување), но, кај повеќето алгоритми, нема никаква логика. Најлошото време на извршување е многу поедноставно за пресметка, а и ни нуди гаранции за текот на операциите.
На пример, што ако имаме две програми кои се поставени на два компјутери поврзани на Интернет и истите се повикуваат од посетители на некој сајт. Притоа, едната програма има просечно време на извршување од 1 секунда и најлошо време на извршување од 2 секунди, додека другата програма има просечно време на извршување од 0.02 секунди и најлошо време на извршување од 200 секунди. Втората програма, во просек, е многу побрза од првата - но може да предизвика сериозен проблем доколку се појават податоци поради кои таа би работела 200 секунди. Тогаш, ќе мора да се чека 200 секунди за некој следен посетител да може да прави пресметки. Сега, замислете дека работите за Google и споредувате алгоритми за пребарување на податоци - сигурно веднаш ќе ги отфрлите алгоритмите кои треба да се извршуваат со минути. Од друга страна пак, ако можете да ја откриете поврзаноста на влезните податоци со времето на извршување, тогаш можете од двата алгоритми да направите еден нов алгоритам кој ќе ги поседува и двата атрибути - одлично просечно време на извршување и одлично најлошо време на извршување.
Проблемот што го дискутиравме погоре (откривање на најголем цел број) може да се реши и со друг алгоритам. Следнава програма има најлоша временска сложеност O(N):
Програма 18.3
#include <iostream>
using namespace std;
int main()
{
int n, t, najgolem = -1;
cin >> n;
for (int i=0; i<n; i++)
{
cin >> t;
if (t > najgolem)
najgolem = t;
}
cout << najgolem << endl;
return 0;
}
Сега може да заклучиме што ни овозможува анализата на временската сложеност - да споредиме два алгоритми кои решаваат еден ист проблем и без да ги пишуваме програмите на компјутер. Денешните компјутери можат да извршат околу 100 000 000 операции за 1 секунда (зборуваме за основните операции дефинирани на почетокот - наредбите за читање, печатење, аритметичките операции, итн...). Знаејќи го овој податок и временската сложеност на еден алгоритам, можеме да пресметаме, за дадени ограничувања на влезните податоци, дали една програма ќе заврши во потребните временски рамки или не. На пример, алгоритам со сложеност O(N) може, без никакви потешкотии, да реши проблем на откривање на најголема вредност во низа со 50 000 елементи.
Пребарување на податоци
Да замислиме дека е потребно да напишеме програма која, за N студенти (на пример, 20 посетители на некој курс), ќе ги отпечати нивните е-маил адреси. Студентите се чуваат во низа student, која е составена од податоци од тип Student - се чува број на индекс, име, презиме, е-маил и телефон. Основниот дел од програмата би изгледал вака:
Извадок 18.2
int N;
cin >> N;
for (int i=0; i < N; i++)
{
//za kogo treba da najdeme e-mail?
int indeks;
cin >> indeks;
//najdi e-mail
string email = najdiEMail(indeks);
cout << "Emailot na studentot so indeks " << indeks << " e " << email << endl;
}
Колкава е сложеноста на овој дел од кодот? Според сé што дискутиравме досега, сложеноста е O(N), така? Имаме еден for циклус кој чита број на индекс за N студенти и ги печати нивните е-маил адреси.
Погрешно! Бидејќи не знаеме колку операции ќе се извршат во функцијата najdiEMail(int indeks), гледајќи го само овој дел од програмата и не можеме да заклучиме колкава е сложеноста на алгоритамот. Многу е веројатно во функцијата за наоѓање на е-маил да постои некој циклус кој би се движил низ низата student и би пребарувал студенти со одреден број на индекс:
Извадок 18.3
string najdiEMail(int indeks)
{
for (int i=0; i<brojStudenti; i++)
if (student[i].indeks == indeks)
return student[i].email;
return "GRESHKA! Nema takov student.";
}
Дури сега можеме да дадеме заклучок за сложеноста на алгоритамот за наоѓање на e-mail адреси за N студенти - тоа е O(N*M), каде N е бројот на студенти за кои треба да најдеме e-mail адреса, а M е вкупниот број на студенти во системот (во горниот дел од кодот, тоа е променливата brojStudenti).
Дали постои начин на кој може да го подобриме алгоритамот? Доколку студентите се ставени во низа која не е подредена според бројот на индекс, тогаш немаме друг избор: мора да го извршуваме горенаведениот алгоритам - почнувајќи од првиот студент, за секој проверуваме дали неговиот број на индекс е еднаков на бараниот.
Но, што доколку студентите се подредени според број на индекс? Во тој случај, постои начин на кој може да се подобри програмата. Како? Па, на сличен начин како што бараме телефонски број во телефонски именик: да го искористиме фактот што податоците се подредени. Кај телефонскиот именик најпрвин се појавуваат податоци за луѓе чие презиме започнува на буквата А, па за оние чие презиме започнува на буквата Б, итн. Доколку има повеќе луѓе со иста прва буква од презимето, се врши подредување по втората буква од презимето, итн.
Како бараме телефонски број во телефонски именик? Еден начин на кој може да пребаруваме оди вака: Доколку именикот има 2 000 000 записи, провери го 1 000 000 запис (оној во средината). Да речеме дека 1 000 000 запис е човек со име "Марковски Петар". Ако имаме неверојатно многу среќа и сме го погодиле точно човекот кој го бараме, тогаш го враќаме неговиот број. Но, доколку тоа не е човекот што го бараме, може веднаш да елиминираме голем број од записите - ако бараното лице е во првата половина од именикот (на пример, презимето на човекот што го бараме почнува на буква која во азбуката се наоѓа пред M), можеме веднаш да отфрлиме половина од именикот (втората половина). Слично, доколку човекот е во втората половина, можеме да ја отфрлиме првата половина од именикот. Доколку ја повторуваме оваа постапка (наречена бинарно пребарување) повеќе пати - неверојатно многу брзо ќе дојдеме до бараниот телефонски број. На пример, за телефонски именик со 2 000 000 записи, потребно е да направиме најмногу 21 споредба.
Конкретно, за телефонски именик со 1 запис - потребна е една споредба. За именик со 2 записи, потребни се 2 споредби. За именик со 3 записи, потребни се (најмногу) 2 споредби. Понатаму:
- за именик со 7 записи, потребни се најмногу 3 споредби.
- за именик со 15 записи, потребни се најмногу 4 споредби.
- за именик со 127 записи, потребни се најмногу 7 споредби.
- за именик со 1023 записи, потребни се најмногу 10 споредби.
- за именик со 1048575 записи, потребни се најмногу 20 споредби.
- за именик со 1073741823 записи, потребни се најмногу 30 споредби.
Забележете колку бавно расте оваа функција. За алгоритмите со вакво однесување се вели дека имаат логаритамска сложеност O(logN) - бидејќи обратната математичка функција од степенување (cx) се нарекува логаритмирање. Не е важна основата на логаритамот - на сличен начин како што ги отфрлавме константите во претходните анализи, сега може да делиме на 2 дела, на 3 дела или на 10 - сложеноста повторно ќе биде O(logN).
Проблем на патувачки трговец
Проблемот на патувачки трговец може да се дефинира на следниот начин: за дадена листа од градови и растојанија помеѓу нив, потребно е да го најдеме најкраткиот пат кој ќе го посети секој од градовите по точно еднаш.
На пример, да ги разгледаме можните патеки за N=3 градови (Париз, Мадрид и Лондон).
(1 -> 2 -> 3) Париз -> Мадрид -> Лондон
(1 -> 3 -> 2) Париз -> Лондон -> Мадрид
(2 -> 1 -> 3) Мадрид -> Париз -> Лондон
(2 -> 3 -> 1) Мадрид -> Лондон -> Париз
(3 -> 1 -> 2) Лондон -> Париз -> Мадрид
(3 -> 2 -> 1) Лондон -> Мадрид -> Париз
За N=3 градови имаме вкупно 6 можни патеки. За N=4 имаме 24 можни патеки. За N=5 имаме 120, за N=6 имаме 720, za N=7 имаме 5040, за N=8 имаме 40320, ..., за N=20 имаме 2432902008176640000 патеки, итн. Доколку должината на патеките не зависи од насоката (должината од Лондон до Париз е еднаква на должината од Париз до Лондон), можно е да скокнеме дел од патеките - но нишно значително.
Математички, зборуваме за операција наречена факториел - N!
3! = 3*2*1 = 6
4! = 4*3*2*1 = 24
5! = 5*4*3*2*1 = 120
6! = 6*5*4*3*2*1 = 720
Доколку го решаваме овој проблем така што ќе ги анализираме сите патеки и на крајот ќе ја одбереме најкратката, сложеноста на алгоритамот е О(N!).

Преземено (линк) од xkcd.com според CC BY-NC 2.5 лиценца.
Во следната табела се дадени сите сложености кои ги споменавме досега, како и други сложености кои често се среќаваат при решавање на алгоритамски задачи:
| име | сложеност | пример |
|---|---|---|
| константна сложеност | O(1) | проверка дали еден број е делив со 10 |
| логаритамска сложеност | O(logN) | пронајди елемент во подредена низа |
| линеарна сложеност | O(N) | пронајди елемент во неподредена низа |
| NlogN сложеност | O(NlogN) | подредување на низа од броеви (следи подолу) |
| квадратна сложеност | O(N2) | читање на елементи на квадратна матрица |
| експоненцијална сложеност | O(xN) | генерирање на сите подмножества |
| факториелна сложеност | O(N!) | решавање на проблемот на патувачки трговец преку испитување на сите можни патеки |
Подредување на елементи на низа
Да го разгледаме следниот проблем: дадена ни е низа од N елементи [5, 4, 2, 1, 5, 3] и потребно е истата да ја доведеме во растечки [1, 2, 3, 4, 5, 5] или опаѓачки [5, 5, 4, 3, 2, 1] редослед. (Во многу книги на македонски јазик се зборува за т.н. "сортирање" на низа, но јас ќе го користам терминот "подредување").
Да започнеме со следниот алгоритам (за подредување во растечки редослед): за секоја позиција во низата (почнувајќи од 0 и завршувајќи со N-1) пронајди го елементот кој треба да се наоѓа на таа позиција во низата и смести го таму. За време на извршување на алгоритамот, низата (виртуелно) ќе се подели на два дела: подреден дел (на почетокот на низата) и неподреден дел (на крајот од низата - тоа се всушност елементите кои сеуште не сме ги сместиле на точната позиција). Во литературата, овој алгоритам е познат под името "подредување преку одбирање" (анг. selection sort).
Извадок 18.4
void sort(int niza[], int N)
{
for (int i=0; i<N; i++)
{
//pretpostavi deka min e na pozicija i
int min = i;
for (int j=i+1; j<N; j++)
if (niza[j] < niza[min])
min = j; //nov minimum
if (min != i) //zameni
{
int temp = niza[i];
niza[i] = niza[min];
niza[min] = temp;
}
}
}
Анализата на временската сложеност е едноставна: за секоја од N-те позиции во низата треба да направиме споредба на тековниот елемент со околу N/2 елементи (оние елементи кои се наоѓаат десно од него). За првиот елемент (niza[0]) треба да направиме N-1 споредба, за вториот (niza[1]) треба да направиме N-2 споредби, итн. до последниот елемент за кој треба да направиме 0 споредби (тој сигурно е на точната позиција, бидејќи е последен елемент и нема со кого да го споредуваме). Збирот е 0 + 1 + 2 + 3 + ... + (N-1), што е збир на елементите на позната аритметичка прогресија (првите X природни броеви) и изнесува 0 + 1 + 2 + 3 + ... + (N-1) = (N*(N-1)) / 2. Значи, алгоритамот има временска сложеност O(N2).
Следниот алгоритам кој ќе го разгледаме е познат под името подредување со метод на меурче (анг. bubble sort). Овој алгоритам работи преку замена на соседни елементи кои се наоѓаат во погрешен редослед. Името на алгоритамот доаѓа од таму што помалите елементи испливуваат (како меурчиња) до врвот на листата. И тој, како и алгоритамот претставен претходно, има квадратна временска сложеност O(N2).
Извадок 18.5
void sort(int niza[], int N)
{
bool premestuva = true;
while (premestuva)
{
premestuva = false;
for (int i=1; i<N; i++)
if (niza[i-1] > niza[i])
{
int temp = niza[i-1];
niza[i-1] = niza[i];
niza[i] = temp;
premestuva = true;
}
}
}
Анализата на временската сложеност на овој алгоритам е малку потешка од онаа на претходниот алгоритам - бидејќи сега имаме циклус за кој не знаеме колку пати ќе се изврши. Всушност, почетната позиција на елементите има мнооогу значајна улога при одредувањето на времето на извршување на овој метод. Доколку низата е веќе подредена, сложеноста е линеарна O(N), и тоа е најдоброто време на извршување на алгоритамот. Доколку имаме големи елементи на почетокот [5, 1, 2, 3, 4, 5], тие не претставуваат сериозен проблем бидејќи брзо се преместуваат до нивната крајна позиција. Но, доколку имаме мали елементи на крајот од низата [2, 3, 4, 5, 5, 1], тие многу бавно се движат до почетокот. На пример, за да се подреди низата [2, 3, 4, 5, 5, 1] потребен е квадратен број на операции. Во просек, подредувањето со методот на меурче е еден од најбавните алгоритми за подредување - околу 40% е побавен од претходниот алгоритам (подредување преку одбирање).
Сега, да се обидеме да ја анализираме временската сложеност на уште еден алгоритам: алгоритамот за подредување со соединување (анг. merge sort). Merge sort претставува рекурзивен алгоритам за подредување кој работи на т.н. "раздели-па-владеј" принцип. Гледано од аспект на временската сложеност, рекурзивните алгоритми се едни од најтешките за анализирање.
Конкретно, алгоритамот за подредување со соединување работи на следниот начин:
- низата се дели на два (релативно) еднакви дела
- овие два дела рекурзивно се подредуваат (се повикува истата функција, но за помала низа)
- двата (подредени) дела се соединуваат
Накратко, (скицата на) алгоритамот изгледа вака:
Извадок 18.6
merge_sort(niza[], n)
{
if (n <= 1)
vrati niza
podeli ja niza[] na dve nizi levo[] i desno[]
so (relativno) ednakov broj na elementi
merge_sort(levo)
merge_sort(desno)
soedini gi levo[] i desno[] za da dobiesh
podredena verzija od nizata niza[]
vrati ja podredenata verzija od niza[]
}
Колку време е потребно за да поделиме една низа L на две помали низи S1 и S2? Очигледно, одговорот е O(N) - треба само да ги изминеме сите елементи од низата L, и доколку еден од елементите се наоѓа во првата половина од низата него да го додадеме на S1, а доколку се наоѓа во втората половина од низата да го додадеме на S2.
Но, што со соединувањето? Колкава е сложеноста на постапката на соединување на две (веќе) подредени низи S1 и S2 во една низа L? И тука, сложеноста е O(N) - започнуваме со празна низа L и, во секој чекор, го додаваме најмалиот елемент од S1 или S2: овој елемент секако ќе се наоѓа на почетокот на една од тие две низи. На пример, нека S1[5] = {1, 4, 6, 7, 8} и S2[4] = {1, 2, 3, 6}. Почнуваме со споредување на првите елементи од низите S1 (1) и S2 (1) и го додаваме помалиот од нив во L (нека тоа биде 1 од S1). Потоа, го споредуваме вториот елемент од S1 (4) со првиот елемент од S2 (1) - тоа се најмалите елементи кои сеуште не се додадени во L. Го додаваме помалиот од нив (1 од S2) во L. Продолжуваме со истата постапка се додека не стигнеме до крајот на двете низи. Забележете дека, доколку стигнеме до крајот на една од низите, но не и до крајот на другата, потребно е да ги додадеме сите преостанати елементи од едната низа во L. На пример, за S1[5] = {1, 2, 3, 4, 5} и S2[4] = {6, 7, 8, 9}, прво ќе се додадат сите елементи од S1 во L, а потоа и сите од S2.
Во продолжение е даден кодот на овој алгоритам за подредување - не се обидувајте да го учите кодот на памет! Програмата, во споредба со сето она што сме го виделе досега, е прилично тешка за разбирање. Не се разочарувајте доколку не можете да сфатите како таа работи, или сте обземени од нејзината големина. Дополнително, со цел да се поедностави процесот на соединување, програмата резервира многу повеќе меморија отколку што е тоа потребно за точно решавање на проблемот.
Програма 18.4
#include <iostream>
using namespace std;
//soedini gi nizite left[] i right[], i smesti go rezultatot vo array[]
void merge(int left[], int leftSize, int right[], int rightSize, int array[]);
void sort(int array[], int N)
{
if (N <= 1)
return /* void */;
//podeli na dva dela [0..M-1, M..N-1]
int M = N/2;
//od 0 do M-1 ima tocno M elementi
int leftSize = M;
//od M do N-1 ima tocno N-M elementi
int rightSize = N-M;
int *left = new int[leftSize];
for (int i=0; i<leftSize; i++)
left[i] = array[i];
int *right = new int[rightSize];
for (int i=M; i<N; i++)
right[i-M] = array[i];
//podredi gi pomalite delovi
sort(left, leftSize);
sort(right, rightSize);
//soedini gi left[] i right[] vo array[]
merge(left, leftSize, right, rightSize, array);
//izbrishi gi nizite left[] i right[] (koi gi alociravme dinamicki)
delete [] left;
delete [] right;
}
void merge(int left[], int leftSize, int right[], int rightSize, int array[])
{
int leftCurrent=0, rightCurrent=0, arrayCurrent = 0;
while (leftCurrent < leftSize && rightCurrent < rightSize)
{
//ima ushte elementi i vo left[] i vo right[]
if (left[leftCurrent] < right[rightCurrent])
{
//zemi element od levata niza
array[arrayCurrent] = left[leftCurrent];
arrayCurrent++;
leftCurrent++;
}
else
{
//zemi element od desnata niza
array[arrayCurrent] = right[rightCurrent];
arrayCurrent++;
rightCurrent++;
}
}
while (leftCurrent < leftSize)
{
//nema vekje elementi vo desnata niza, no ima li vo levata?
array[arrayCurrent] = left[leftCurrent];
arrayCurrent++;
leftCurrent++;
}
while (rightCurrent < rightSize)
{
//nema vekje elementi vo levata niza, no ima li vo desnata?
array[arrayCurrent] = right[rightCurrent];
arrayCurrent++;
rightCurrent++;
}
}
int main()
{
int N = 8;
int array[] = {2, 7, 5, 6, 4, 8, 1, 3};
sort(array, 8);
for (int i=0; i<N; i++)
cout << array[i] << " ";
return 0;
}
Најлесен начин да ја анализираме сложеноста на алгоритамот за подредување со соединување (merge sort) е преку исцртување на дрво на повикување на самата рекурзивна функција. Притоа, секое делче (јазол) од дрвото ќе одговара на еден проблем кој го решава рекурзивниот алгоритам. Нормално, првиот (горниот) јазол, т.е. коренот на дрвото, ќе одговара на оригиналниот проблем кој треба да се реши - бидејќи тој го претставува првиот повик до функцијата за подредување. Гранките (помеѓу јазлите) во дрвото ќе одговараат на рекурзивните повици. Кога една функција ќе се повика самата себеси двапати (со два помали подпроблеми), во дрвото ќе имаме еден јазол поврзан со два други јазли (деца) преку гранки кои ги означуваат рекурзивните повици.
Во продолжение е дадено дрвото на повикување на функцијата sort за низата {2, 7, 5, 6, 4, 8, 1, 3}. Тоа е истата низа која ја користевме во програмата дадена погоре.
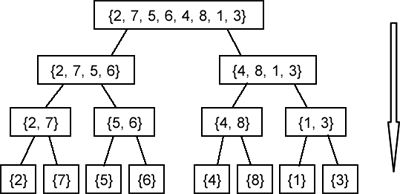
Очигледно, дрвото кое што го прикажавме е идеален случај - користиме низа која што има 8 елементи (8 = 23, односно 8 е степен на бројот 2). Кога ќе имаме низа со број на елементи кој не е степен на 2, дел од рекурзивните повици побрзо ќе стигнат до конечниот услов (број на елементи во низата помал од 1) и решавањето (за тој подпроблем) ќе заврши, наместо во нивото K, во нивото K-1. Ова нема никакво влијание на точноста на нашата анализа.
Процесот на соединување е прикажан на следното дрво (како движење наназад):
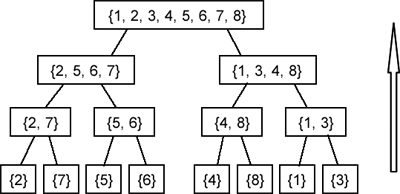
Не е тешко да забележиме дека (во секое од нивоата) работиме со точно N елементи, и дека врз секој елемент (во едно ниво) извршуваме константен број на операции (ја читаме вредноста на елементот при делењето на низата и при нејзиното соединување).
Во првото (најгорното) ниво, работиме со N елементи: кога ја делиме низата на две низи со околу N/2 елементи и кога ги соединуваме двете помали низи во една низа од N елементи. Слично, во последното ниво работиме со точно N елементи (крајот на секој од N-те повици на функциите - кога всушност и констатираме дека сме завршиле со рекурзивните повици). Со N елементи работиме и во претпоследното ниво - потребно е да соединиме N низи од по 1 елемент во N/2 низи од по 2 елементи. Аналогно на ова - може да заклучиме дека во секое ниво од дрвото работиме со точно N елементи.
Останува уште да пресметаме колку нивоа има дрвото. Потоа, ќе може да заклучиме дека сложеноста на алгоритамот е O(M*N), каде М е бројот на нивоа, додека N е бројот на елементи. Ова е точно бидејќи, во секое од M-те нивоа работиме константен број на операции врз точно N елементи. Што се однесува до бројот на нивоа, овој проблем веќе го решивме кога зборувавме за барањето на телефонски број во телефонски именик - потребни се најмногу logN делења за да се изолира одреден елемент.
Конечно, доаѓаме до заклучок дека временската сложеност на алгоритамот за подредување со соединување е O(N*logN).




