Подредување на елементи
Во претходните неколку предавања, зборувавме за разни податочни структури. Притоа, забележавме дека кај обичните низи, како и низите со динамичка големина, можен е ефикасен пристап во константно време O(1) до елементи на произволна позиција (array[0], array[5], итн). Во ова предавање, ќе разгледаме неколку алгоритми за подредување на елементи во низа. Најчесто, вие нема да ги користите овие алгоритми директно, туку ќе подредувате низи со помош на функцијата sort(), која е дел од Стандардната библиотека на шаблони и која веќе имплементира ефикасен алгоритам за подредување на елементи.
Сепак, во повеќето книги кои зборуваат за алгоритми и податочни структури, постои дискусија за разните алгоритми за подредување на елементи, па тоа ќе се обидеме да го направиме и тука. Во ова предавање, ќе научиме што значи терминот стабилно подредување, и како истото може да се направи во програмскиот јазик C++. Покрај ова, ќе разгледаме и како, во случај кога ни се познати некои ограничувања во однос на податоците кои ги подредуваме (на пример, сите се цели броеви од 1 до 10), како е можно да напишеме и алгоритам кој е поефикасен од она што е имплементирано во Стандардната библиотека на шаблони. Дополнително, разгледувањето како повеќе разни алгоритми решаваат еден ист проблем, и како секој од нив има свои предности и недостатоци, ќе ни овозможи покомотно да дискутираме за разни други алгоритми во следните предавања, како и за нивната сложеност. Притоа, во сите примери, ќе ги подредуваме елементите во растечки редослед – обратното се прави со превртување на соодветните оператори за споредба (помало, поголемо) во самиот алгоритам, или со користење на reverse() за превртување на елементите по подредувањето на низата.
Подредување преку одбирање
Еден од поедноставните алгоритми за подредување е т.н. алгоритам за подредување преку одбирање (eng. selection sort). Притоа, постапката е исклучително едноставна: за секоја позиција во низата (почнувајќи од 0 и завршувајќи со N-1) го пронаоѓаме елементот кој треба да се наоѓа на таа позиција во низата и истиот го сместуваме таму. Овој алгоритам има квадратна временска сложеност O(N2).
Извадок 7.1
void sort(int niza[], int N)
{
for (int i=0; i<N; i++)
{
//pretpostavi deka min e na pozicija i
int min = i;
for (int j=i+1; j<N; j++)
if (niza[j] < niza[min])
min = j; //nov minimum
if (min != i) //zameni
{
swap(niza[i], niza[min]);
}
}
}
Ако соодветно го разгледаме алгоритамот, ќе забележиме дека, за време на извршување на истиот, низата (виртуелно) ќе се подели на два дела: подреден дел (на почетокот на низата) и неподреден дел (на крајот од низата - тоа се всушност елементите кои сеуште не сме ги сместиле на точната позиција). Од кога ќе бидат разгледани сите N елементи, веќе не постои неподреден дел, па алгоритамот успешно завршил со решавање на проблемот.
Анализата на временската сложеност е едноставна: за секоја од N-те позиции во низата треба да направиме споредба на тековниот елемент со околу N/2 елементи (оние елементи кои се наоѓаат десно од него). За првиот елемент (niza[0]) треба да направиме N-1 споредба, за вториот (niza[1]) треба да направиме N-2 споредби, итн. до последниот елемент за кој треба да направиме 0 споредби (тој сигурно е на точната позиција, бидејќи е последен елемент и нема со кого да го споредуваме). Збирот е 0 + 1 + 2 + 3 + ... + (N-1), што (математички) е збир на елементите на позната аритметичка прогресија (првите X природни броеви) и изнесува 0 + 1 + 2 + 3 + ... + (N-1) = (N*(N-1)) / 2. Значи, алгоритамот има временска сложеност O(N2).
Се разбира, постојат алгоритми кои многу поефикасно го решаваат проблемот на подредување на елементи во една низа. На крајот од ова предавање, ќе разгледаме и дел од нив.
Меурчиња
Следниот алгоритам кој ќе го разгледаме е познат под името подредување со метод на меурче (анг. bubble sort). Овој алгоритам работи преку замена на соседни елементи кои се наоѓаат во погрешен редослед. Името на алгоритамот доаѓа од таму што помалите елементи испливуваат (како меурчиња) до врвот на листата. И тој, како и алгоритамот претставен претходно, има квадратна временска сложеност O(N2). Во продолжение, ќе разгледаме и еден интересен проблем кој може да се реши со користење на овој метод. Најпрвин, да видиме како изгледа овој алгоритам напишан во програмскиот јазик C++.
Извадок 7.2
void sort(int niza[], int N)
{
bool changes = true;
while (changes)
{
changes = false;
for (int i=1; i<N; i++)
if (niza[i-1] > niza[i])
{
swap(niza[i-1], niza[i]);
changes = true;
}
}
}
Анализата на временската сложеност на овој алгоритам е малку потешка од онаа на претходниот - бидејќи сега имаме циклус за кој не знаеме колку пати ќе се изврши. Всушност, почетната позиција на елементите има мнооогу значајна улога при одредувањето на времето на извршување на овој метод. Доколку низата е веќе подредена, сложеноста е линеарна O(N), и тоа е најдоброто време на извршување на алгоритамот. Доколку имаме големи елементи на почетокот [5, 1, 2, 3, 4, 5], тие не претставуваат сериозен проблем бидејќи брзо се преместуваат до нивната крајна позиција (за овој пример, може да го прочитате кодот и да видите дека првата 5-ка ќе дојде на точното место уште во првото извршување на while циклусот). Но, доколку имаме мали елементи на крајот од низата [2, 3, 4, 5, 5, 1], тие многу бавно се движат до почетокот. На пример, за да се подреди низата [2, 3, 4, 5, 5, 1] потребен е квадратен број на операции – што е она и што највеќе не интересира при анализа на временската сложеност (најлошото време). Во просек, подредувањето со методот на меурче е еден од најбавните алгоритми за подредување – според некои анализи направени на разни сајтови, истиот е околу 40% побавен од претходниот алгоритам (подредување преку одбирање).
Интересно, бидејќи овој алгоритам заменува само соседни елементи во низата, бројот на замени на елементи (swap операции) кои ќе бидат направени со овој алгоритам, е најмалиот број на потребни замени на соседни елементи за подредување на една низа. Поради тоа, доколку додадеме уште една променлива која брои колку пати правиме замени, можеме да дадеме одговор на интересни прашања, како на пример: за време на една трка во Формула 1, колку претекнувања се направени ако колите се движат со константна брзина (т.е., ако не е возможно кола B да ја претекне колата A, ако веќе A ја претекнало B)?
Подредување со соединување
Сега, да се обидеме да ја анализираме временската сложеност на уште еден алгоритам: алгоритамот за подредување со соединување (анг. merge sort). Поради тоа што истиот е многу поефикасен во подредување на елементи, овој алгоритам се користи многу почесто од претходните два. Merge sort претставува рекурзивен алгоритам кој работи на т.н. "раздели-па-владеј" принцип. Гледано од аспект на временската сложеност, рекурзивните алгоритми се едни од најтешките за анализирање. Затоа, овој дел од предавањето ќе биде малку подолг од претходните, но во истиот ќе разгледаме како да споиме две подредени низи во една, како и други интересни проблеми. Притоа, целта не е да го научиме алгоритамот, туку само да видиме како истиот генерално работи, и колку е тешко, кај некои алгоритми, да се анализира временската сложеност.
Притоа, за да разберете како функционира овој алгоритам, потребно е да знаете што е тоа рекурзија. Предавање за истото, и како една функција може да се повикува самата себеси, има во другиот курс на овој сајт, кој содржи предавања за основите на програмскиот јазик C++.
Конкретно, алгоритамот за подредување со соединување работи на следниот начин:
- низата се дели на два (релативно) еднакви дела
- овие два дела рекурзивно се подредуваат (се повикува истата функција, но за помала низа)
- двата (подредени) дела се соединуваат
Главната идеја е дека доколку имаме две помали низи кои се веќе подредени (на пример, една која е еднаква на {3, 7}, и друга на {5, 9}), тогаш можеме едноставно истите да ги споиме и да добиеме нова низа која е исто така подредена ({3, 5, 7, 9}). Ова е објаснето подолу. Целта на користењето на рекурзијата е да направиме вакви помали низи, и потоа истите да ги спојуваме во поголеми. Накратко, (скицата на) алгоритамот изгледа вака:
Извадок 7.3
merge_sort(niza[], n)
{
if (n <= 1)
vrati niza
podeli ja niza[] na dve nizi levo[] i desno[]
so (relativno) ednakov broj na elementi
merge_sort(levo)
merge_sort(desno)
soedini gi levo[] i desno[] za da dobiesh
podredena verzija od nizata niza[]
vrati ja taa podredena verzija kako rezultat
}
Колку време е потребно за да поделиме една низа L на две помали низи S1 и S2? Очигледно, одговорот е O(N) - треба само да ги изминеме сите елементи од низата L, и доколку еден од елементите се наоѓа во првата половина од низата него да го додадеме на S1, а доколку се наоѓа во втората половина од низата да го додадеме на S2.
Но, што со соединувањето? Колкава е сложеноста на постапката на соединување на две (веќе) подредени низи S1 и S2 во една низа L? И тука, сложеноста е O(N) - започнуваме со празна низа L и, во секој чекор, го додаваме најмалиот елемент од S1 или S2: овој елемент секако ќе се наоѓа на почетокот на една од тие две низи. На пример, нека S1[5] = {1, 4, 6, 7, 8} и S2[4] = {1, 2, 3, 6}. Почнуваме со споредување на првите елементи од низите S1 (1) и S2 (1) и го додаваме помалиот од нив во L (нека тоа биде 1 од S1). Потоа, го споредуваме вториот елемент од S1 (4) со првиот елемент од S2 (1) - тоа се најмалите елементи кои сеуште не се додадени во L. Го додаваме помалиот од нив (1 од S2) во L. Продолжуваме со истата постапка се додека не стигнеме до крајот на двете низи. Забележете дека, доколку стигнеме до крајот на една од низите, но не и до крајот на другата, потребно е да ги додадеме сите преостанати елементи од едната низа во L. На пример, за S1[5] = {1, 2, 3, 4, 5} и S2[4] = {6, 7, 8, 9}, прво ќе се додадат сите елементи од S1 во L, а потоа и сите од S2.
Во продолжение е даден кодот на овој алгоритам за подредување - не се обидувајте да го учите кодот на памет! Програмата, во споредба со сето она што сме го виделе досега, е прилично тешка за разбирање. Не се разочарувајте доколку не можете да сфатите како таа работи, или сте обземени од нејзината големина. Дополнително, со цел да се поедностави процесот на соединување, програмата резервира многу повеќе меморија отколку што е тоа потребно за точно решавање на проблемот.
Програма 7.1
#include <iostream>
using namespace std;
//soedini gi nizite left[] i right[], i smesti go rezultatot vo array[]
void merge(int left[], int leftSize, int right[], int rightSize, int array[]);
void sort(int array[], int N)
{
if (N <= 1)
return /* void */;
//podeli na dva dela [0..M-1, M..N-1]
int M = N/2;
//od 0 do M-1 ima tocno M elementi
int leftSize = M;
//od M do N-1 ima tocno N-M elementi
int rightSize = N-M;
int *left = new int[leftSize];
for (int i=0; i<leftSize; i++)
left[i] = array[i];
int *right = new int[rightSize];
for (int i=M; i<N; i++)
right[i-M] = array[i];
//podredi gi pomalite delovi
sort(left, leftSize);
sort(right, rightSize);
//soedini gi left[] i right[] vo array[]
merge(left, leftSize, right, rightSize, array);
//izbrishi gi nizite left[] i right[] (koi gi alociravme dinamicki)
delete [] left;
delete [] right;
}
void merge(int left[], int leftSize, int right[], int rightSize, int array[])
{
int leftCurrent=0, rightCurrent=0, arrayCurrent = 0;
while (leftCurrent < leftSize && rightCurrent < rightSize)
{
//ima ushte elementi i vo left[] i vo right[]
if (left[leftCurrent] < right[rightCurrent])
{
//zemi element od levata niza
array[arrayCurrent] = left[leftCurrent];
arrayCurrent++;
leftCurrent++;
}
else
{
//zemi element od desnata niza
array[arrayCurrent] = right[rightCurrent];
arrayCurrent++;
rightCurrent++;
}
}
while (leftCurrent < leftSize)
{
//nema vekje elementi vo desnata niza, no ima li vo levata?
array[arrayCurrent] = left[leftCurrent];
arrayCurrent++;
leftCurrent++;
}
while (rightCurrent < rightSize)
{
//nema vekje elementi vo levata niza, no ima li vo desnata?
array[arrayCurrent] = right[rightCurrent];
arrayCurrent++;
rightCurrent++;
}
}
int main()
{
int N = 8;
int array[] = {2, 7, 5, 6, 4, 8, 1, 3};
sort(array, 8);
for (int i=0; i<N; i++)
cout << array[i] << " ";
return 0;
}
Најлесен начин да ја анализираме сложеноста на алгоритамот за подредување со соединување (merge sort) е преку исцртување на дрво на повикување на самата рекурзивна функција. Притоа, секое делче (јазол) од дрвото ќе одговара на еден проблем кој го решава рекурзивниот алгоритам. Нормално, првиот (горниот) јазол, т.е. коренот на дрвото, ќе одговара на оригиналниот проблем кој треба да се реши - бидејќи тој го претставува првиот повик до функцијата за подредување. Гранките (помеѓу јазлите) во дрвото ќе одговараат на рекурзивните повици. Кога една функција ќе се повика самата себеси двапати (со два помали подпроблеми), во дрвото ќе имаме еден јазол поврзан со два други јазли (деца) преку гранки кои ги означуваат рекурзивните повици.
Во продолжение е дадено дрвото на повикување на функцијата sort за низата {2, 7, 5, 6, 4, 8, 1, 3}. Тоа е истата низа која ја користевме во програмата дадена погоре.
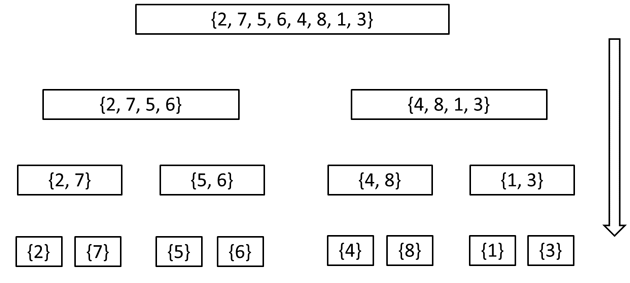
Очигледно, дрвото кое што го прикажавме е идеален случај - користиме низа која што има 8 елементи (8 = 23, односно 8 е степен на бројот 2). Кога ќе имаме низа со број на елементи кој не е степен на 2, дел од рекурзивните повици побрзо ќе стигнат до конечниот услов (број на елементи во низата помал од 1) и решавањето (за тој подпроблем) ќе заврши, наместо во нивото K, во нивото K-1. Ова нема никакво влијание на точноста на нашата анализа.
Процесот на соединување е прикажан на следното дрво (како движење наназад):

Не е тешко да забележиме дека (во секое од нивоата) работиме со точно N елементи, и дека врз секој елемент (во едно ниво) извршуваме константен број на операции (ја читаме вредноста на елементот при делењето на низата и при нејзиното соединување).
Во првото (најгорното) ниво, работиме со N елементи: кога ја делиме низата на две низи со околу N/2 елементи и кога ги соединуваме двете помали низи во една низа од N елементи. Слично, во последното ниво работиме со точно N елементи (крајот на секој од N-те повици на функциите - кога всушност и констатираме дека сме завршиле со рекурзивните повици). Со N елементи работиме и во претпоследното ниво - потребно е да соединиме N низи од по 1 елемент во N/2 низи од по 2 елементи. Аналогно на ова - може да заклучиме дека во секое ниво од дрвото работиме со точно N елементи.
Останува уште да пресметаме колку нивоа има дрвото. Потоа, ќе може да заклучиме дека сложеноста на алгоритамот е O(M*N), каде М е бројот на нивоа, додека N е бројот на елементи. Ова е точно бидејќи, во секое од M-те нивоа имаме операции врз точно N елементи. Што се однесува до бројот на нивоа, овој проблем веќе го решивме кога зборувавме за барањето на телефонски број во телефонски именик (со отварањето на средина отфрламе половина од записите, и со секој следен потег уште по половина од оние записи кои се останати), па потребни се најмногу logN делења за да се изолира одреден елемент (N -> N/2 -> N/4 -> .... 1).
Конечно, доаѓаме до заклучок дека временската сложеност на алгоритамот за подредување со соединување е O(NlogN).
Подредување со броење
Веќе споменавме дека функцијата sort(), која е веќе имплементирана за нас во програмскиот јазик C++, има временска сложеност O(NlogN). Дополнително, постои доказ дека сите алгоритми за подредување кои користат споредба на елементите не може да имаат подобра временска сложеност од O(NlogN).
Но, кај некои проблеми, однапред знаеме одредени ограничувања во самите податоци, и кај кои не мора да правиме споредба (со < и >) помеѓу елементите, што ни овозможува да искористиме интересни алгоритми за подредување кои функционираат и во линеарно време O(N). На пример, замислете дека имаме низа од 1000 елементи, но сите тие се еднакви или на 1, или на 2, или на 3. Во овој случај, можеме само да направиме три променливи count1, count2 и count3, да ја изминеме низата, и да изброиме колку пати се појавува секој од нив. Потоа, само ставаме count1 единици на почетокот во низата, count2 двојки потоа, и на крајот, count3 тројки.
На овој начин функционира т.н. алгоритам за подредување со броење (eng. counting sort). Во случај кога имаме N броеви за подредување, и постојат повеќе различни вредности, но сите се во интервалот од 0 до K (во случајот со примерот погоре, K=3), овој алгоритам има временска сложеност O(N+K).
Извадок 7.4
void sort(int niza[], int N)
{
int input[N];
for (int i=0; i < N; i++)
{
input[i] = niza[i]; //za da mozhe da ja menuvame niza[]
}
int K = 0;
for(int i=0; i<N; i++)
{
if(input[i] > K)
{
K = input[i]; //odredi ja maksimalnata vrednost
}
}
int before[K + 1];
memset(before, 0, sizeof(before));
for (int i=0; i<N; i++)
{
int value = input[i];
before[value]++; //broime kolku pati se pojavuva sekoj broj
}
for (int value=1; value <= K; value++)
{
before[value] += before[value-1]; //kolku elementi ima pred "value"
}
for (int i=N-1; i>=0; i--)
{
before[input[i]]--; //za da pochnuvaat indeksite od 0
int position = before[input[i]];
niza[position] = input[i];
}
}
За секоја вредност, пред последниот for циклус, во низата before[X] чуваме колку елементи во оригиналната низа се помали или еднакви на таа вредност X. На пример, нека знаеме дека моментно разгледуваме вредност еднаква на 3, и нека знаеме дека во оригиналната низа има осум вредности еднакви на 2, и две вредности еднакви на 3. Во тој случај, 10 елементи се помали или еднакви на вредноста 3 (before[3] = 10), па, разгледувајќи го кодот даден погоре, ќе видиме дека тој ќе постави 3-ка на позицијата 10-1=9 во низата со подредени вредности - што е многу логично, бидејќи таа е последната позиција на која можеме да ставиме 3-ка (како што кажавме, имаме и осум 2-ки за кои треба да оставиме простор за тие да бидат поставени). Доколку има и други вредности еднакви на 3, бидејќи правиме намалување на вредноста запишана во before (before[input[i]]--), во понатамошното извршување на for циклусот, истите ќе бидат сместени во некои од помалите индекси (на пример, на индекс 8 во подредената низа).
Иако е ова навистина интересен алгоритам, често подобро е да ја користите функцијата sort() од Стандардната Библиотека на Шаблони (STL). Во скоро сите ситуации, таа работи навистина ефикасно, и нема потреба да се пишуваат дополнителни алгоритми за подредување. Временската сложеност O(NlogN) е една од подобрите кои се среќаваат; па алгоритмите со ваква сложеност функционираат без проблеми и во случаи кога имаме и повеќе од милион елементи (N = 1 000 000). Дополнително, најчесто други делови од кодот кој ќе го пишувате ќе имаат поголема сложеност од оваа, и истите ќе доминираат со времето на извршување земајќи најголем дел од истото.
Интересна примена на бинарните дрва
Како што кажавме, во Стандардната библиотека на шаблони постои имплементација на множество - кое користи бинарно дрво во позадина (за чување на елементите). Бидејќи, кај оваа податочна структура, постои редослед и можност за изминување на елементите почнувајќи од најмалиот (или најголемиот), а знаеме и дека стандардната имплементација на set<> автоматски не дозволува додавање на еден елемент повеќе пати, тогаш можеме во неколку линии код да искористиме трик за подредување на елементи и елиминирање на дупликати. Притоа, бидејќи додавање на елемент во бинарно дрво има логаритамска сложеност O(logN), а ќе имаме N такви додавања за да ги ставиме сите елементи во множеството, временската сложеност на алгоритамот ќе биде O(NlogN), што е слично како и при користење на функцијата sort().
Програма 7.2
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <bits/stdc++.h>
using namespace std;
int main()
{
vector<int> numbers = {1, 3, 2, 5, 4, 7, 7, 8, 8, 6};
set<int> ordered(numbers.begin(), numbers.end());
for(int value : ordered)
{
cout << value << " "; //kje otpechati "1 2 3 4 5 6 7 8"
}
cout << endl;
//ako sakame pak da dobieme vector
vector<int> sorted(ordered.begin(), ordered.end());
for(int value : sorted)
{
cout << value << " "; //kje otpechati "1 2 3 4 5 6 7 8"
}
return 0;
}
Притоа, забележете дека, при создавањето на множеството, нема потреба да ги додаваме (со for) еден по еден елементите, туку тоа може да го направи Стандардната библиотека на шаблони за нас, доколку наведеме покажувачи за делот од кој сакаме да биде составено множеството – во случајот, користиме numbers.begin() и numbers.end() за да означиме дека сакаме да ги земеме сите броеви од низата со динамичка големина numbers.
Стабилно подредување
Понекогаш, при подредување, постојат повеќе критериуми по кои елементите може да се споредуваат еден со друг. На пример, да разгледаме низа од стрингови со следните елементи [“Marko”, “Darko”, “Petar”, “Ana”]. Кај одредени проблеми, ќе сакаме елементите на оваа низа да ги подредиме во алфабетски редослед (како кај речник), но кај други проблеми, можеби ќе сакаме овие елементи да ги подредиме според бројот на знаци (на пример, стрингот “Ana” има три знаци и треба да дојде пред “Darko” кој има 5 знаци). Во претходното предавање, видовме како може да напишеме функција за споредба на самите елементи, со што овој проблем ќе успееме да го решиме едноставно.
Но, можеби забележавте како некои од елементите (во случајов “Marko”, “Darko” и “Petar”) имаат еднаков број на знаци. Притоа, се поставува прашањето – како овие елементи треба да бидат подредени меѓусебно – дали “Darko” да дојде пред “Marko”, или “Marko” пред “Darko”, итн.
Во вакви случаи, постојат неколку можни ситуации кои треба да се разгледаат. Во првата, може воопшто да не не интересира меѓусебниот редослед на овие елементи. Се додека “Ana” ќе дојде на првата позиција, каков меѓусебен редослед во продолжение ќе имаат останатите елементи (“Darko”, “Marko” и “Petar”) може да не ни е воопшто важно. Всушност, ова е и најчестата ситуација - да сакаме да ги подредиме елементите по еден критериум, за потоа да ги разгледуваме во точен редослед по тој (еден) критериум.
Со втората ситуација, исто така знаеме како да се справиме. Имено, понекогаш сакаме редоследот да зависи од еден критериум, а во случај кога елементите се еднакви по тој критериум (во случајов, должината на стрингот) елементите да се подредат по некој друг критериум (на пример, алфабетскиот редослед). Во таков случај, бидејќи имаме функција за споредба во која можеме ова да го напишеме, не постои никаков проблем за реализација на истото.
Програма 7.3
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <bits/stdc++.h>
using namespace std;
bool sort_by_length_and_name(string a, string b)
{
if(a.size() == b.size())
{
//podredi alfabetski
return a < b;
}
//razlicna dolzhina, podredi po toa
return a.size() < b.size();
}
int main()
{
vector<string> names = {"Marko", "Darko", "Petar", "Ana"};
sort(names.begin(), names.end(), sort_by_length_and_name);
for(string name : names)
{
cout << name << " "; //pechati "Ana Darko Marko Petar"
}
return 0;
}
Но, да разгледаме уште една ситуација. Што доколку сакаме елементите да ги подредиме по одреден критериум (на пример, должина на стрингот), а во случај на еднакви елементи по тој критериум - да ги оставиме истите во нивниот првобитен меѓусебен редослед во низата? Со други зборови, ако имаме два стрингови со иста должина 10 во оригиналната низа (пред подредувањето на елементи), да гарантираме дека истите ќе останат во нивниот првобитен меѓусебен редослед (ако едниот стринг се наоѓал пред другиот во оригиналната низа, да се наоѓа пред другиот и во подредената низа). Во ваков случај, велиме дека користиме “стабилно подредување” на елементите (eng. stable sort).
Функцијата sort() од Стандардната библиотека на шаблони не гарантира “стабилно подредување”, туку еднаквите елементи (според критериумите на споредба – на пример, должина) може да завршат во било кој редослед. Доколку ни е важно овие елементи да го задржат нивниот меѓусебен редослед, можеме да ја користиме функцијата stable_sort(), која се повикува со истите параметри. Инаку, стабилното подредување не се користи многу често, бидејќи ретко е важно да се гарантира почетниот редослед, па оваа функција ќе ја користите ретко. Притоа, иако таа има сложеност O(NlogN), поради потребата од задржување на оригиналниот распоред, таа работи малку побавно од sort().
За крај, да се запрашаме како можеме да ја искористиме функцијата sort(), а сепак да гарантираме “стабилно подредување”? Одговорот е едноставен. Имено, секој алгоритам за подредување може да се промени за да гарантира стабилно подредување, доколку ја искористиме почетната позиција на елементите како критериум при подредувањето. Ова можеме да го направиме, во Стандардната библиотека на шаблони, така што ќе направиме пар од вредноста на елементот и неговата позиција, и ќе ги подредиме елементите користејќи ја позицијата како дополнителна информација.
Програма 7.4
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <bits/stdc++.h>
using namespace std;
//se koristi od stable_sort() podolu
bool stable_sort_by_length(string a, string b)
{
return a.size() < b.size();
}
//se koristi od sort() podolu
bool sort_by_length_and_pos(pair<string, int> a, pair<string, int> b)
{
string name_a = a.first;
int pos_a = a.second;
string name_b = b.first;
int pos_b = b.second;
if(name_a.size() == name_b.size())
{
//podredi po pozicija ako imaat ednakva dolzhina
return pos_a < pos_b;
}
//razlichna dolzhina, pa podredi po toa
return name_a.size() < name_b.size();
}
int main()
{
vector<string> names = {"Marko", "Petar", "Ana", "Maja", "Igor", "Darko"};
//opcija 1, koristejki stable_sort()
stable_sort(names.begin(), names.end(), stable_sort_by_length);
//opcija 2, koristejki sort()
vector<pair<string, int> > names_with_position;
for(int i=0; i < names.size(); i++)
{
string name = names[i];
names_with_position.push_back( {name, i} );
}
sort(names_with_position.begin(), names_with_position.end(), sort_by_length_and_pos);
return 0;
}
Иако ретко ќе имате причина да користите “стабилно подредување”, целта на овој дел од предавањето беше да се запознаете со значењето на тој термин, бидејќи истиот се користи во разна литература поврзана со програмирање, алгоритми и податочни структури. При секојдневното пишување на функции и компјутерски програми (на работа, или за време на натпревари), најчесто ќе ја користите функцијата sort(). Како и кај C++, поради тоа што подредувањето на елементи е често барање при решавање на проблеми, во останатите програмски јазици (како Java и други) постојат функции со исто или слично име, кои овозможуваат лесно и ефикасно подредување, со минимален напор од наша страна.




