Во ова предавање, ќе продолжиме со разгледување на неколку проблеми кои може да се решат со техниката на динамичко програмирање. Дополнително, ќе обрнеме внимание на фактот дека еден ист проблем може да се реши на повеќе различни начини, и како (прецизно) да одредиме кое решение е подобро во соодветната ситуација. Покрај одредување на најдобрата вредност кај еден проблем, ќе видиме и како да ги откриеме потезите, предметите или елементите кои не водат до таа вредност. На пример, доколку сакаме да откриеме колку најмалку пари треба да потрошиме за да стигнеме од Скопје до Лос Анџелес, покрај самата сума, можеби не интересира и кои (авионски) карти треба да ги земеме за да може да го испланираме патувањето. Во продолжение, ќе ги разгледаме овие поими и идеи подетално, фокусирајќи се на два исклучително познати проблеми кои може да се решат со техниката на динамичко програмирање: проблемот на ранец, и проблемот на откривање на најдолга заедничка подниза (објаснето подолу). Па, да започнеме.

Проблем на ранец

Најпрвин, да го дефинираме проблемот кој што ќе го решаваме. Имено, нека имаме неколку предмети, и нека за секој предмет ни е позната неговата тежина (на пример, во килограми), и неговата вредност (на пример, во денари). Доколку имаме ранец кој има капацитет од C килограми, која е најголемата вредност која што можеме да ја постигнеме ако го направиме најдобриот избор на предмети кои ќе ги ставиме во ранецот?

На пример, ако имаме ранец со капацитет од 10 килограми, и избор од три предмети, каде првиот предмет има тежина од 9 килограми и вредност од 3000 денари, вториот предмет има тежина од 5 килограми и вредност од 2000 денари, а третиот предмет има тежина од 3 килограми и вредност од 1500 денари, најдобро решение е да ги земеме последните два предмети, кои имаат вкупна тежина од 8 килограми, и вредност од 3500 денари. Во ранецот не можеме да ги сместиме сите три предмети, бидејќи нивната вкупна тежина е 17 килограми (што е повеќе од капацитетот на ранецот C).

Како да го решиме овој проблем? Очигледно, бидејќи во насловот на ова предавање се споменува динамичко програмирање, ќе разгледаме алгоритми кои ја користат таа техника. Но, за разлика од претходните проблеми кои ги сретнавме, а се решаваа со помош на динамичко програмирање, тука имаме мал проблем. Имено, бидејќи сме ограничени по капацитетот на ранецот (на пример, 10 килограми), а кај динамичко програмирање зборувавме за решавање на помали проблеми (ги нарекувавме состојби), и користење на решенијата на тие состојби за решавање на оригиналниот проблем, веројатно очекувате состојбата да е големината на ранецот. Па, доколку знаеме кое е најдобро решение за ранци со капацитет 1, 2, 3, 4, 5, 6, 7, 8, и 9, да можеме да го најдеме и решението за ранец со капацитет 10. За жал, кај овој проблем сме ограничени и по однос на предметите. Имено, освен големината на ранецот, треба да знаеме и кои предмети веќе ги имаме земено, бидејќи секој предмет можеме да го земеме само еднаш (на пример, ако имаме една книга, една тетратка и еден лаптоп, не можеме во ранецот да сместиме два лаптопи).

Во вакви случаи, можеме да ја дефинираме состојбата по однос на повеќе параметри. На пример, лесно ќе дојдеме до решение доколку состојбата која што ќе ја користиме, покрај големината на ранецот, означува и кои предмети веќе ги имаме разгледано. Па така, доколку знаеме кое е најдоброто решение за ранци каде се разгледани првите два предмети и сите големини на ранци од 1 до 10, лесно можеме да дојдеме до решенијата каде го разгледуваме и третиот предмет и разни големини на ранци. Со други зборови, ако веќе сме разгледале два предмети и сме одлучиле кои од нив е најдобро да се земат (можеби и двата, доколку ги собира истите) за сите можни ранци со капацитет од 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10, и разгледуваме нов предмет и големина на ранец, само треба да одлучиме дали е подобро да го земеме третиот предмет, или да не го земеме. Доколку не го земеме третиот предмет, вредноста ќе биде иста како и со разгледани два предмети - а доколку го земеме, ќе ја зголемиме и вредноста, но и искористениот капацитет за чување на предметите.

На пример, доколку во моментот го разгледуваме третиот предмет (кој, на пример, има тежина од 3 килограми) и разгледуваме големина на ранец од 7 килограми, прво не интересира кое е најдоброто решение каде ги имаме разгледано првите два предмети. Ако не го земеме третиот предмет, вредноста ќе биде иста како онаа каде се разгледани првите два предмети, и не ни треба поголем ранец. Втората опција која што ја имаме е да го земеме третиот предмет. Во тој случај, не интересира најдоброто решение за првите два предмети и помал ранец со капацитет од 4 (7-3) килограми - бидејќи, ако веќе имаме пресметано кои предмети да ги сместиме во ранец со капацитет од 4 килограми, тогаш знаеме дека за земање на третиот предмет кој има тежина од 3 килограми, ќе ни треба ранец со капацитет од точно 7 килограми (што сакаме да го пресметаме во овој момент). Притоа, единствено што треба да се вметне во алгоритамот е одлуката која од овие две опции (да се земе предметот, или да не се земе) е подобра.

(На сликата, best[3][7] означува кое е најдоброто решение ако се разгледуваат првите 3 предмети, и ранец со капацитет 7.)

За чување на решенијата за состојби кои имаат повеќе параметри, најчесто користиме повеќедимензионални низи. Па така, best[X][C] може да ни означува која е најдобрата вредност која сме ја постигнале за ранец со капацитет од C килограми, разгледувајќи ги само првите X предмети. За примерот што го разгледавме погоре, конечната вредност која ја бараме ќе биде best[3][10], односно најдобрата вредност која може да се постигне за ранец со капацитет од 10 килограми, кога веќе се разгледани сите 3 предмети. Алгоритамот за решавање на овој проблем ќе изгледа вака:

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;

//weight[i] e tezhinata na i-tiot predmet
//value[i] e vrednosta na i-tiot predmet
int knapsack(vector<int> &weight, vector<int> &value, int capacity)
{
     int N = weight.size();
     
     //napravi matrica, i postavi se ednakvo na 0
     int best[N+1][capacity+1];
     memset(best, 0, sizeof(best));
     
     //pochni so razgleduvanje na prviot predmet, pa na prvite dva, itn...
     for(int x=1; x <= N; x++)
     {
          int objectWeight = weight[x - 1];   //bidejki prviot element ima indeks 0
          int objectValue = value[x - 1];     //bidejki prviot element ima indeks 0
          
          //razgledaj ranci so razlichen kapacitet...
          for(int c=0; c <= capacity; c++)
          {
               //ako ne go zememe x-tiot predmet
               int leaveValue = best[x-1][c];
               best[x][c] = leaveValue;
               
               if(objectWeight <= c)
               {
                    //predmetot ne e pogolem od ranecot
                    //obidi se da go zemesh...
                    int takeValue = best[x-1][c - objectWeight] + objectValue;
                    
                    if(takeValue > leaveValue)
                    {
                         //podobro reshenie e da go zememe predmetot
                         best[x][c] = takeValue;
                    }
               }
          }
     }
     
     return best[N][capacity];
}


int main()
{
     vector<int> weight = {9, 5, 3};
     vector<int> value = {3000, 2000, 1500};
     
     cout << knapsack(weight, value, 10) << endl;
     return 0;
}

Во програмата дадена погоре, користиме две низи со динамичка големина, weight и value, за чување на тежината и вредноста на секој од предметите. Овој избор е направен со цел кодот да е полесен за читање и разбирање. Друга опција е да користиме пар од вредности pair<int, int>, каде, на пример, првиот елемент од парот (.first) ќе ја означува тежината, а вториот (.second) ќе ја означува вредноста. Како резултат од функцијата, ја добиваме најголемата вредност која што може да се постигне при најдобриот можен избор на предмети кои ќе ги ставиме во ранецот.

Доколку се немате сретнато со неа порано, можеби ќе ве збуни користењето на функцијата memset, за поставување на нула на сите вредности во една низа (со една или повеќе димензии). Во C++, променливите имаат недефинирана вредност се додека не им доделиме конкретен податок за чување. Како што видовме и во претходното предавање за динамичко програмирање, при користењето на оваа техника, во алгоритмите дефинираме основни (или тривијални) случаи, чиј резултат ни е однапред познат. Во овој пример, познато ни е дека ранец, во случајот кога имаме разгледано 0 предмети, ќе содржи предмети во вредност од 0 денари (бидејќи нема да има ниту еден предмет во него), па потребно е сите елементи best[0][...] да ги поставиме на 0. Бидејќи memset ни дозволува ефикасно да ја пополниме и целата матрица (наместо само неколку вредности), ние ги поставивме сите елементи во матрицата да бидат еднакви на 0 (иако тоа не е потребно).

Одбирање на предмети

Решението за проблемот на ранец, кое што го напишавме погоре, ни овозможи да ја откриеме најголемата вредност која што може да се постигне при најдобриот избор на предмети кои може да ги земеме во ранецот. Сепак, како што може да се забележи и од самата дефиниција на функцијата во решението, тоа ни ја дава само најголемата можна вредност, како бројка. Но, што доколку сакаме да откриеме и кои предмети треба да ги земеме за да ја постигнеме таа најголема вредност? Дали треба да ги земеме првиот и третиот предмет, само првиот предмет, или некоја друга комбинација од предмети?

За утврдување на изборот кој води до постигнување на одредена вредност, кај техниката на динамичко програмирање, најчесто имаме две опции: разгледување на состојбите, или користење на дополнителна податочна структура за чување на изборот на предмети. Притоа, ова не важи само за овој конкретен проблем, туку опциите кои ги споменавме ќе ги користиме и при решавање на други задачи со динамичко програмирање.

Разгледување на состојбите. Кога решаваме проблеми со техниката на динамичко програмирање, за откривање на решението користиме повеќе состојби - т.е. решенија на други (помали) проблеми. Многу често, бидејќи на располагање ги имаме решенијата за сите овие состојби, можеме лесно да го откриеме изборот кој води до најдоброто решение за главниот проблем кој го решаваме. Под главен проблем, зборуваме за конечното решение кое сме го откриле - во нашиот случај, проблемот за целиот ранец, каде се разгледани сите предмети. Притоа, кај скоро сите проблеми, до изборот се доаѓа многу полесно доколку ги разгледуваме состојбите почнувајќи од крајот - т.е. од вредноста која што го дава решението за главниот проблем.

За проблемот на ранец кој што го решававме, ако замислиме дека имаме три предмети на располагање, и дека капацитетот на ранецот е 10 килограми, ова значи дека треба да почнеме од таа крајна состојба best[3][10]. Сега, за да знаеме дали треба да го земеме третиот предмет, треба само да провериме дали вредноста на best[3][10] е еднаква на best[2][10]. Доколку вредноста best[3][10] е поголема од best[2][10], знаеме дека треба да го земеме третиот предмет, бидејќи тој придонел за зголемување на најголемата вредност (која што алгоритамот ја открил). Притоа, бидејќи практично се враќаме наназад во решението, пред да прејдеме на разгледување на следниот предмет (во овој случај, вториот), а во претходниот чекор сме одлучиле да го земеме третиот предмет, сега треба да разгледаме состојба со помал капацитет за сместување на преостанатите предмети - т.е. доколку големината на третиот предмет е 5, во следниот чекор ќе ја разгледуваме состојбата [3-1][10-5], односно најдоброто решение каде ги разгледуваме првите 2 предмети, и ранец со големина 5. Причината за ова е фактот што, во следните чекори, не интересира кој од следните предмети да ги земеме, но за нив имаме само капацитет 5 за нивно сместување - бидејќи веќе сме одлучиле да го земеме третиот предмет. Оваа постапка ја повторуваме за сите 3 предмети (за третиот, за вториот, и за првиот предмет), и, на тој начин, доаѓаме до листата од предмети кои треба да се земат во ранецот.

Забележете дека оваа идеја не можеме да ја примениме почнувајќи од првиот елемент. Напротив, мораме да почнеме од крајот (кога веќе ни се разгледани сите предмети), со одење наназад (3, 2, 1). Причината за ова е јасна - имено, додека не ги разгледаме сите предмети не можеме да знаеме која е најдобрата вредност. Напротив, можеби баш последниот предмет ќе има огромна вредност, па без разлика што претходните состојби велеле дека дотогаш е најдобро да се земе првиот предмет, тоа ќе се промени со последниот чекор. Како што наведовме, имајте предвид дека, практично секогаш, за соодветен избор потребно е да се почне од крајната состојба.

vector<int> knapsackItems(vector<int> &weight, vector<int> &value, int capacity)
{
     int N = weight.size();
     
     int best[N+1][capacity+1];
     memset(best, 0, sizeof(best));
     
     for(int x=1; x <= N; x++)
     {
          int objectWeight = weight[x - 1];
          int objectValue = value[x - 1];
          
          for(int c=0; c <= capacity; c++)
          {
               int leaveValue = best[x-1][c];
               best[x][c] = leaveValue;
               
               if(objectWeight <= c)
               {
                    int takeValue = best[x-1][c - objectWeight] + objectValue;
                    
                    if(takeValue > leaveValue)
                    {
                         best[x][c] = takeValue;
                    }
               }
          }
     }
     
     vector<int> items;
     int currentCapacity = capacity;
     
     for(int x=N; x >= 1; x--)
     {
          if(best[x][currentCapacity] > best[x-1][currentCapacity])
          {
               //indeksite pochnuvaat od 0
               items.push_back(x - 1);    //oznachi deka go zemame elementot
               currentCapacity -= weight[x - 1];
          }
     }
     
     return items;
}

Погоре, нема никакви промени во самиот алгоритам, туку само додадовме код на крајот за откривање на изборот на предмети. Овојпат, функцијата (наместо најголемата вредност, како број) враќа низа со динамичка големина, која го содржи потребниот избор на предмети. Во конкретниот случај, функцијата ќе врати [2, 1], што значи дека треба да ги земеме третиот и вториот предмет (нормално, бидејќи се движиме наназад, овие бројки се во обратен редослед).

Користење дополнителна податочна структура. Втората опција која што може да ја искористиме за утврдување на изборот на предмети е користењето на дополнителна меморија за чување на самите потези кои ги правиме. Притоа, зависно од проблемот кој го решаваме, можеме да користиме низи, мапи, или било која друга податочна структура која делува најсоодветна. Кај повеќето проблеми со кои ќе се среќаваме, оваа опција (користењето на дополнителна податочна структура) е подобра, и нуди поедноставни и попрегледни решенија (иако, најчесто, кодот ќе изгледа многу сличен како и со првата опција). Дополнително, важно е да се наведе дека покрај запишувањето во дополнителни податочни структури, и тука тргнуваме со разгледување од крајот - т.е., од состојбата која го дефинира решението на главниот проблем.

Поконкретно, во нашето решение треба да направиме две промени. Најпрвин, во самиот алгоритам, при правењето на одреден избор (дали да земеме предмет или не), ќе додадеме нова наредба која го запишува направениот избор во друга низа (да ја наречеме истата choice). Притоа, сами може да одредиме дека choice[x][c]=1 означува дека x-тиот предмет треба да го земеме кога разгледуваме ранец со големина c, a choice[x][c]=0 означува дека не треба да го земеме истиот (наместо 1 и 0, може да користиме било кои други вредности).

Следно, по завршувањето на пресметките (кога веќе се разгледани сите состојби), тргнуваме од крајната состојба која го дефинира главниот проблем, и се враќаме наназад гледајќи ги направените избори (кои ни се зачувани во низата choice).

vector<int> knapsackItems(vector<int> &weight, vector<int> &value, int capacity)
{
     int N = weight.size();
     
     int best[N+1][capacity+1];
     memset(best, 0, sizeof(best));
     
     int choice[N+1][capacity+1];             //nova linija
     memset(choice, 0, sizeof(choice));       //nova linija
     
     for(int x=1; x <= N; x++)
     {
          int objectWeight = weight[x - 1];
          int objectValue = value[x - 1];
          
          for(int c=0; c <= capacity; c++)
          {
               int leaveValue = best[x-1][c];
               best[x][c] = leaveValue;
               choice[x][c] = 0;               //nova linija, ne zemaj
               
               if(objectWeight <= c)
               {
                    int takeValue = best[x-1][c - objectWeight] + objectValue;
                    
                    if(takeValue > leaveValue)
                    {
                         best[x][c] = takeValue;
                         choice[x][c] = 1;               //nova linija, zemi
                    }
               }
          }
     }
     
     vector<int> items;
     int currentCapacity = capacity;
     
     for(int x=N; x >= 1; x--)
     {
          if(choice[x][currentCapacity] == 1)
          {
               //indeksite pochnuvaat od 0
               items.push_back(x - 1);
               currentCapacity -= weight[x - 1];
          }
     }
     
     return items;
}

Забележете дека овој код е многу сличен на претходниот. Единствено, наместо да споредуваме две вредности (со x-тиот предмет, и без него), тука имаме низа која означува дали да го земеме предметот или не. Кај некои проблеми, двете решенија ќе бидат слични едно на друго (како што се тука). Кај други проблеми, каде што има повеќе опции (наместо само две - дали да земеме предмет или не), вториот начин ќе биде поедноставен. Целта на ова предавање, и овој пример, е да ги наведеме овие два начина за одредување на изборот на предмети/потези - за да можете вие, кога ќе се сретнете со друг проблем, да можете да одлучите кој од нив е посоодветен за примена во таа ситуација.

Други решенија за проблемот на ранец

Погоре, при решавање на проблемот на ранец (откривањето на најголемата вредност која што можеме да ја постигнеме), користевме матрица за вредностите кај секоја состојба, каде покрај капацитетот на ранецот, го имавме и бројот на разгледани предмети. Но, дали постои начин состојбата да ни е само капацитетот на ранецот, со што ќе можеме да користиме обична низа и многу помалку меморија за решавање на истиот проблем? Како што споменавме погоре, главната пречка за тоа е фактот што предметите можеме да ги земеме само по еднаш, па при разгледувањето на помали и поголеми состојби, важно е да внимаваме да не земеме еден предмет повеќе пати.

Пред да видиме како може да го постигнеме тоа, да пробаме да го решиме проблемот каде што еден предмет може да се земе и по повеќе пати. Во ваков случај, алгоритамот кој ќе го напишеме треба да има основна состојба (тоа може да биде фактот дека најдобрата вредност за разгледани 0 предмети е 0 денари, бидејќи нема ништо во ранецот), и алгоритамот, за одреден капацитет и предмет, треба да одлучи дали е подобро да се земе тој предмет или не. Слично како и претходно, тоа го правиме со разгледување на помалата состојба за ранец со капацитет (c - objectWeight), бидејќи од таа состојба, со земање на предметот може да стигнеме до состојба каде капацитетот на ранецот е еднаква на c. Да го видиме решението.

int knapsack(vector<int> &weight, vector<int> &value, int capacity)
{
     int N = weight.size();
     
     int best[capacity+1];
     memset(best, 0, sizeof(best));
     
     for(int x=1; x <= N; x++)
     {
          int objectWeight = weight[x - 1];
          int objectValue = value[x - 1];
          
          for(int c=0; c <= capacity; c++)
          {
               if (objectWeight <= c)
               {
                    //predmetot ne e pogolem od ranecot
                    int takeValue = best[c - objectWeight] + objectValue;
                    if(takeValue > best[c])
                    {
                         best[c] = takeValue;
                    }
               }
          }
     }
     
     return best[capacity];
}

Забележете како best[] е сега обична низа, наместо матрица. На овој начин, користиме помалку меморија. За разлика од претходно, сега може да се случи еден предмет да го сместиме и повеќе пати. Дополнително, забележете како best[c] може да се пребрише (со нови вредности) повеќе пати, бидејќи секој капацитет c го разгледуваме за сите x предмети.

Сега, да се вратиме на првобитниот проблем. Имено, во решението дадено погоре, кога разгледуваме одреден предмет и капацитет (на пример, предмет со тежина 3, и ранец со капацитет 3), можеме да одлучиме да го земеме тој предмет, и да ја запишеме неговата вредност во best[3]. Следно, кога ќе дојде на разгледување ранец со капацитет 6, можеби повторно ќе го земеме тој предмет, па во best[6]=(best[3] + вредноста на предметот). Со други зборови, во best[6] ќе биде сместена двапати вредноста на предметот (како да сме го земале двапати). Како да го смениме нашиот код, за ова да не се случува - т.е., да знаеме дека секој предмет може да се земе само по еднаш? Интересно, решението на овој проблем е исклучително едноставно. Имено, она што треба да направиме е, во вториот for циклус, наместо да се движиме од 0 до capacity, да се движиме во обратен редослед (од capacity до 0). На овој начин, ќе го елиминираме точно примерот кој го дадовме погоре - да не може при разгледување на капацитет од 3, и понатаму на капацитет од 6, вредноста таму да означува збир од вредноста на еден ист предмет по повеќе пати. Едноставно, ова нема да се случи доколку прво разгледаме ранец со капацитет од 6, па дури потоа ранец со капацитет од 3. При разгледувањето на ранец со капацитет од 6, вредноста во best[3] ќе ја означува најголемата вредност која може да се постигне со претходните предмети (без оној кој го разгледуваме во моментот).

int knapsack(vector<int> &weight, vector<int> &value, int capacity)
{
     int N = weight.size();
     
     int best[capacity+1];
     memset(best, 0, sizeof(best));
     
     for(int x=1; x <= N; x++)
     {
          int objectWeight = weight[x - 1];
          int objectValue = value[x - 1];
          
          for(int c=capacity; c >= 0; c--)    //promeneta linija
          {
               if (objectWeight <= c)
               {
                    int takeValue = best[c - objectWeight] + objectValue;
                    if(takeValue > best[c])
                    {
                         best[c] = takeValue;
                    }
               }
          }
     }
     
     return best[capacity];
}

Зависно од проблемот кој го решавате, некои алгоритми се посоодветни од другите. На пример, последното решение што го наведовме користи помалку меморија (само низа) од првото решение на проблемот (кое користеше матрица). Од друга страна пак, кај тоа решение беше едноставно да се напише код за добивање на самите предмети кои треба да се земат во ранецот - додека кај ова решение, тоа ќе претставува многу поголем проблем - бидејќи, кога се движиме наназад, некои предмети може да ги запишеме повеќе пати, за ранци со различни капацитети. На пример, при разгледување на првиот предмет, ако тој има тежина од 3, вредноста ќе се запише и кај ранец со капацитет 10, 9, 8, 7, 6, 5, 4, и 3. Иако вредноста ќе биде иста на секоја позиција (како да сме го земале предметот по еднаш), овој факт ќе ни претставува проблем при враќањето наназад и одбирањето на самите предмети (доколку тоа сакаме да го направиме).

Зависно од самиот проблем, на вас останува да одберете или напишете алгоритам кој е најсоодветен за негово решавање. Најчесто, компјутерите имаат доволно меморија за чување на повеќе вредности, па и понеефикасни алгоритми може да бидат доволни – нормално, тоа зависи од самите вредности, бројот на предмети и слично. Во конкретниот случај, и двата алгоритми кои ги разгледавме се користат често - и истите можете да ги сретнете, како при решавање, така и во разна литература (курсеви, сајтови, книги и слично).

Други форми на проблемот на ранец

Како што веќе споменавме, проблемот на ранец е исклучително познат (како оној со дозволено земање на предмет по повеќе пати, така и оној со земање по еднаш), и истиот ќе го среќавате при решавањето на разни проблеми. На пример, да замислиме дека имаме само 30000 денари, и сакаме да купиме неколку книги од Amazon. За секоја книга ја знаеме нејзината цена (во денари), и колку истата ни значи (на пример, број од 1 до 10). Доколку сакаме да купиме повеќе книги, а средствата кои ни се располагање (во овој случај, 30000 денари) ги сметаме како капацитет на еден ранец, оваа задача можеме да ја решиме преку едноставна примена на алгоритамот за решавање на проблемот на ранец. Слично, алгоритамот можеме да го примениме и на многу други проблеми и задачи.

Внимавајте, иако во оригиналниот текст на проблемот се споменува ранец и негов капацитет во вид на тежина, ова не значи дека истиот треба да го научиме на памет и да го применуваме само кога ќе забележиме проблем каде што се споменува ранец. Целта на овие предавања (и на многу други), е да се запознаеме со неколку проблеми и нивните решенија - со цел, во иднина, кога ќе сретнете нов проблем, да успеете да го примените тоа знаење. Притоа, одбирањето на алгоритам и поврзувањето со проблеми кои веќе ги имате сретнато се прави преку пронаоѓање на сличности помеѓу проблемите. Во овој случај, без разлика дали зборуваме за ранец со капацитет даден во килограми, или за ограничен буџет за купување на книги, имаме проблем каде ни се дадени повеќе предмети, и треба да направиме избор на дел од нив поради фактот што сме ограничени по некој основ (капацитет на ранец, лимитирани парични средства, итн).

Најдолга заедничка подниза

Подниза на S е низа која што може да се добие со бришење на неколку знаци од S, без притоа да го менуваме распоредот на останатите знаци (притоа, може да зборуваме за низи од цифри, обични стрингови и слично). На пример, доколку S=”zdravo”, тогаш “z”, “zr”, “zo”, “rvo”, и “davo” се поднизи на S, бидејќи до секоја од нив можеме да дојдеме доколку избришеме неколку знаци од S.

Заедничка подниза е подниза која се појавува во два стрингови. На пример, “rvo” е заедничка подниза на “zdravo” и “mrzlivo”, бидејќи се појавува (како подниза) во двата стрингови. Ако ни се дадени стрингови S и T, дали можеме да ја најдеме должината на најдолгата заедничка подниза на S и T? На пример, за следните два стрингови S=”ABAXDM” и T=“BAMBADZ”, најдолгата заедничка подниза e “ABAD”. “ABAD” има должина 4, и е подниза и на S, и нa Т.

Истиот овој проблем можеме да го објасниме и на друг начин. Имено, ако ги напишеме стринговите S и T еден под друг, она што се бара од нас во проблемот е да нацртаме што е можно повеќе линии помеѓу еднакви знаци во S и T, така што линиите нема да се сечат една со друга – впрочем, како што е нацртано на сликата.

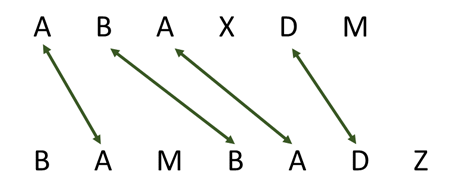
Овој проблем се користи во многу области, вклучувајќи биоинформатика и пронаѓање на направени промени во документи или датотеки. Истиот може да се реши со помош на динамичко програмирање. За решавање, како и кај сите други примери кои ги видовме, може да почнеме со дефинирање на состојбите (помалите верзии од истиот проблем), и да определиме како тоа ќе ни помогне за да дојдеме до конечното решение. Па, да почнеме.

Најпрвин, може да забележиме дека тука имаме два стрингови (S и T), и секој од нив е составен од повеќе знаци. Дополнително, очигледно е дека, при обидите да пронајдеме заеднички знаци во S и во T, ќе ни биде важно да знаеме до кој знак сме стигнати во едниот стринг, како и до кој знак сме стигнати во другиот стринг (како инаку ќе знаеме што да споредуваме?). Ова не води до констатација дека состојбата треба да зависи од два параметри: позицијата до каде сме стигнати во S, и позицијата до каде сме стигнати во T. Доколку за чување на резултатите користиме матрица length[x][y], која ни означува колку изнесува должината на најдолгата заедничка подниза на S и T ако досега сме ги разгледале сите знаци во S до x-тиот и сите знаци во T до y-тиот, конечниот резултат кој го бараме ќе се наоѓа во таа матрица, на позиција length[должина на S][должина на T] - т.е., кога веќе се разгледани сите знаци. Значи, ни преостанува да откриеме кои се основните (тривијални) состојби, и како да решиме нова состојба користејќи ги резултатите на претходните.

Јасно е дека, ако во S сме разгледале 0 знаци, или пак во T сме разгледале 0 знаци, дека не сме пронашле ниту еден знак кој се наоѓа во двата стрингови - имено, во еден од нив не сме ни разгледале знак, па како може да сме нашле нешто што се наоѓа на две места? Поради тоа, можеме да кажеме дека length[x][0] = 0, и length[0][y] = 0, за било кој број x и y. Кај повеќето проблеми, откривањето на вакви тривијални состојби е едноставно – имено, истото најчесто се базира на состојби кои означуваат дека нешто сеуште не е разгледано (како во случајов, каде од стринг сме разгледале 0 знаци), или пак дека е разгледан само еден знак, предмет или елемент (па таму, вредноста која ќе ја сместиме во низата или матрицата ќе биде, на пример, 1).

Сега, како може да откриеме кое е решението за одредена состојба length[x][y]? Ако оваа состојба не можеме да ја поврземе со претходните, тогаш имаме проблем - и треба да бараме друго решение (со некоја друга техника, или друг начин на запишување на состојбите). За да дојдеме до одговорот на ова, треба да се запрашаме кои се можните ситуации кои може да се случат, кога го разгледуваме x-тиот знак од S (нека го наречеме S[x]), и y-тиот знак од T (нека го наречеме T[y])? Па, може да се случат две ситуации: тие два знака да се еднакви, или да се различни.

Притоа, доколку се еднакви, ќе сакаме тој (еднаков) знак да е дел од заедничката подниза, бидејќи истиот се наоѓа и во S (на позиција x), и во T (на позиција y). Бидејќи во дадениот момент ги разгледуваме тие два знака, јасно е дека нема логика, доколку се истите еднакви, да решиме да не го додадеме тој знак на заедничката подниза - едноставно, зошто да го прескокнеме, кога веќе сакаме да ја најдеме најдолгата заедничка подниза? Тука, во однос на самата вредност, ќе имаме дека length[x][y] = length[x-1][y-1] + 1, бидејќи должината ќе биде еднаква на најголемата должина која може да се постигне се до (x-1)-вата позиција во S (целата должина на S се до x-тиот знак, но без него), и (y-1)-вата позиција во T (целата должина на T се до y-тиот знак, но без него), зголемена за 1 (за знакот кој го пронајдовме дека се наоѓа во двата стрингови). Едноставно, замислете вака: веќе знаеме колку најмногу знакови може да поврземе се до позиција x во S, и позиција y во Т, и сега ни доаѓа на разгледување знак кој се наоѓа во двата стрингови. Должината на заедничката подниза зависи од тоа колку знакови сме поврзале се до таму, зголемена за 1 - поради новиот еднаков знак кој го пронајдовме во двата стрингови.

Во ред, но што доколку двата знакови S[x] и T[y] се разликуваат? Тука, имаме две опции – да го прескокнеме (да не го поврземе со ништо) x-тиот знак од S, или да го прескокнеме y-тиот знак од T. За да знаеме кој од нив да го прескокнеме, доволно е да ги разгледаме состојбите length[x-1][y] и length[x][y-1], и да ја земеме поголемата од нив. Во length[x-1][y] ја имаме должината на најдолгата заедничка подниза кога се разгледани сите знаци без x-тиот од S (па знаеме колку ќе изнесува вредноста на length[x][y] ако сакаме да го прескокнеме знакот S[x]), а во length[x][y-1] ја имаме должината кога се разгледани сите знаци без y-тиот во T (па знаеме колку ќе изнесува вредноста на length[x][y] ако сакаме да го прескокнеме знакот T[y]). Притоа, овие две состојби веќе ги имаме пресметано, бидејќи истите доаѓаат пред length[x][y]. Поради ова, во самиот алгоритам може едноставно да кажеме дека, ако x-тиот знак од S не е еднаков на y-тиот знак од T, имаме length[x][y] = max(length[x-1][y], length[x][y-1]). Забележете дека решивме да прескокнеме само еден знак (x-тиот од S, или y-тиот од T), а не и двата - бидејќи некој од нив би можел, во продолжение на алгоритамот, да се поврзе со друг знак (на пример, x-тиот од S да се поврзе со (y+1)-виот знак од T).

int longestCommonSubsequence(string &S, string &T)
{
     int length[S.length() + 1][T.length() + 1];
     memset(length, 0, sizeof(length));
     
     for(int x=0; x <= S.length(); x++)
     {
          for(int y=0; y <= T.length(); y++)
          {
               if(x == 0 || y == 0)
               {
                    //ne mora da koristime memset koga go
                    //imame ovoj del, ama sepak... (toa e dobra vezhba)
                    length[x][y] = 0;
               }
               else 
               {
                    //x-tiot znak vo S e na pozicija (x-1), bidejki pochnuvaat od 0
                    //slichno vazhi i za T
                    if(S[x-1] == T[y-1])
                    {
                         length[x][y] = length[x-1][y-1] + 1;
                    }
                    else
                    {
                         length[x][y] = max(length[x-1][y], length[x][y-1]);
                    }
               }
          }
     }
     
     return length[S.length()][T.length()];
}

Забележете дека, иако динамичкото програмирање е една од покомплицираните техники за разбирање (и многу луѓе имаат потешкотии со нејзино сфаќање), сите проблеми кои ги разгледавме досега се решаваа на сличен начин. Имено, кај сите имавме состојби, тривијални случаи, редоследно разгледување на предмети (или знаци), и користење на дополнителна меморија (низи, матрици, мапи и слично) за чување на решенијата за разните состојби. Имајте ги во предвид овие елементи при решавањето на други проблеми со техниката на динамичко програмирање, и ќе забележите дека многу работи ќе ви делуваат познати.

Решавање на други проблеми

Како што видовме од повеќето проблеми кои ги решававме, идејата која што се користи кај техниката на динамичко програмирање е едноставна: почнувајќи со идентификување на состојбите на проблемот и како тие се поврзани меѓусебно, можеме да напишеме равенки кои означуваат како од една состојба се доаѓа до друга (слично како и кај рекурзијата). Поентата кај динамичкото програмирање е да ги зачувуваме решенијата на состојбите, за истите да не ги пресметуваме повторно и повторно. Доколку успееме да го направиме ова, временската сложеност на решението ќе зависи од вкупниот број на состојби, што е најчесто она што сакаме да го постигнеме.

Доколку сте заинтересирани за учество во натпревари по информатика, не би требало да ве изненади фактот дека, на истите, се појавуваат многу задачи кои се решаваат со техниката на динамичко програмирање. Причината за ова е фактот дека натпреварите најчесто траат само по неколку часа, па на нив не може да се даваат задачи за кои треба да се пишуваат долги решенија. Кај динамичкото програмирање, решенијата се најчесто кратки (во однос на должината на програмскиот код), и главната потешкотија е да откриеме кои се состојбите и како се тие меѓусебно поврзани. Што повеќе вежбате, и што повеќе задачи решавате, тоа полесно ќе можете да се снајдете за време на самиот натпревар.

Дозвола за користење: CC BY-NC 2.5 ©