Граф е математичка структура која се користи за претставување на врски/релации помеѓу одредени објекти. На пример, со помош на граф можеме да претставиме како одредени лица се поврзани меѓусебно на социјалната мрежа Facebook (кој е пријател со кого), како градовите се поврзани меѓусебно со патишта, но и да ги претставиме врските кај електричните мрежи, водоводните мрежи, и слично. Понатаму, со помош на алгоритми кои се специјално дизајнирани за работа со графови истите можеме и да ги анализираме. Во продолжение, ќе се запознаеме со основните поими кај теоријата на графови, но и како истите можеме да ги претставиме при пишувањето на компјутерски програми. Бидејќи теоријата на графови опфаќа повеќе поими, но и бидејќи истата може да се користи за решавање на значаен број на проблеми, теоријата ќе ја воведуваме постапно – имено, покрај ова предавање, и следните неколку предавања ќе разгледуваат теми поврзани со графовите – наоѓање на најкраток пат, поврзување со минимална цена, итн.

Темиња, ребра и типови на графови

Во дефиницијата за граф дадена погоре, споменавме објекти и дека истите може меѓусебно да се поврзани со врски/релации. Во продолжение, бидејќи во скоро секоја стручна литература се користат истите називи, ќе ги користиме термините теме (за означување на објекти), и ребро (за означување на врските помеѓу темињата). На пример, доколку разгледуваме пријателства помеѓу различни лица на социјалната мрежа Facebook, и сакаме истите да ги претставиме со помош на граф, темињата ќе бидат луѓето - а, за секое пријателство, ќе нацртаме ребро од едното до другото лице. Нормално, веројатно ќе имаме повеќе пријателства, па во графот ќе нацртаме онолку ребра колку што има парови на лица кои се пријатели. Еден ваков пример е даден на следната слика.

Забележете како ребрата (линиите) помеѓу темињата немаат стрелка (т.е. насока). За овие графови велиме дека се неориентирани графови. Покрај ваквите графови, постојат и такви каде што на секое ребро му придружуваме и насока – на пример, доколку сакаме да нацртаме граф во кој темињата претставуваат градови, а ребрата патишта помеѓу тие градови (забележете како, одредени патишта во државата се еднонасочни – може да се патуваат само во една насока). За ваквите графови велиме дека истите се ориентирани графови. Тука, многу е важно да забележиме дека помеѓу две темиња можно е да постојат и повеќе ребра. На пример, во случајот кој го споменавме погоре, каде што зборувавме за градови и патишта помеѓу нив, сосема е нормално (и често), да постојат повеќе патишта помеѓу два града – на пример, едниот во една насока, а другиот во друга насока; или пак, стар пат и понов пат. Ова е претставено на следната слика.

Иако веќе споменавме повеќе термини (темиња, ребра, неориентирани и ориентирани графови), што е доволно за да можете да разберете голем дел од работите за кои ќе зборуваме во продолжение, сепак е важно, во овој дел, да го споменеме и поимот тежински граф. Имено, при анализирање на различни проблеми кои може да се претстават со помош на граф, може да се соочиме со ситуација каде што е потребно на самите ребра кои ги поврзуваат темињата да им придружиме некоја вредност (тежина, далечина или нешто друго). На пример, ако зборуваме за градови и патишта, можеби ќе имаме информации за должината на самите патишта (на пример, дека патот од Скопје до Тетово е долг 40 километри, итн). Како што напоменавме и погоре, ваквите графови каде што за секое ребро е дефиниран и одреден реален број кој ја означува неговата тежина, растојание, или некоја друга слична мерка, се нарекуваат тежински графови.

Сликите кои што ги цртаме од разни графови не мора точно да ги претставуваат сите делови, насоки или вредности во графот. Имено, единственото нешто што ни е важно при цртањето на графот е да ги обележиме сите информации кои ќе ни бидат нам потребни за претставување или решавање на одреден проблем. Сликите не мора да се совршени, и многу често постојат повеќе начини да се нацрта еден граф – на пример, одредено теме наместо лево да го нацртаме на десната страна од графот (нормално, точно зачувувајќи ги врските со останатите темиња), итн.

Циклуси, дрва

Два други термини кои може да ги слушнете при дискутирањето на разни графови се циклуси и дрва. Циклус претставува пат во еден граф каде што, тргнувајќи од едно теме и патувајќи низ графот, можеме повторно да се вратиме кај истото тоа теме. На пример, ако разгледуваме патишта во една држава, циклус може да претставува патот Скопје -> Куманово -> Велес -> Скопје (да тргнеме од Скопје, па од таму да патуваме до Куманово, па од Куманово до Велес, па од Велес до Скопје). Најчесто, при решавањето на разни задачи поврзани со графовите, ќе забележиме дека истите многу полесно се решаваат доколку графот не содржи циклуси. Сепак, како што видовме во примерот погоре, голем број од графовите содржат еден или повеќе циклуси. За наша среќа, скоро сите алгоритми кои ќе ги разгледаме во наредните неколку предавања (а кои се поврзани со графови), функционираат и на графови кои содржат циклуси.

Дрво претставува неориентиран граф (ребрата немаат насока), каде што темињата се меѓусебно поврзани со точно еден пат (не постои повеќе од еден начин да се стигне од било кое теме до било кое друго теме). Нормално, ова значи и дека дрвата не содржат циклус, но и дека истите имаат точно (N – 1) ребро, каде што N е бројот на темиња. Имено, точно (N-1) ребро се потребни за да се поврзат N темиња, на начин што постои точно еден пат помеѓу било кои две темиња во тој граф.

Претставување на граф

Кога ќе пишуваме програми кои работат со графови, ќе ни треба начин за да ги претставиме самите графови во компјутерска меморија – на пример, кои темиња се поврзани со кои други темиња со ребра. Иако постојат повеќе начини на кои ова може да се изведе, ние ќе се фокусираме на двата најмногу споменувани начини: користење на матрица на соседство (што може да се користи кога работиме со графови кои имаат релативно мал број на темиња), и користење на листи на соседство (ова е начинот кој ќе го користиме ние, при пишувањето на сите алгоритми кои ќе ги споменуваме почнувајќи од наредното предавање).

Да разгледаме најпрвин како можеме да претставиме еден граф со помош на матрица на соседство. Имено, да замислиме дека имаме граф со N темиња (каде N е релативно мал број – на пример, до 100). Во ваков случај, можеме да направиме матрица со големина N*N, каде секој елемент од матрицата ij (i-ти ред, j-та колона) ќе означува дали постои ребро помеѓу i-тото теме и j-тото теме (доколку имаме тежински граф, запишаната вредност во матрицата може да биде тежината на реброто). На пример, на следната матрица е претставен граф од 5 темиња, и врските помеѓу нив:

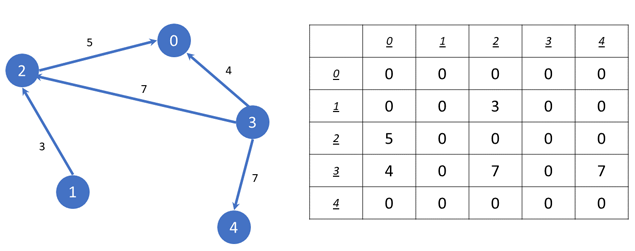
Најпрвин, забележете дека матрицата има големина 5x5 (5 редови и 5 колони), бидејќи графот е составен од 5 темиња. Во матрицата постојат повеќе елементи еднакви на 0 (може да се користи и бројот -1, или нешто слично), со што означуваме дека не постои ребро помеѓу тој пар на темиња. Од друга страна пак, да го разгледаме елементот во матрицата каде што е запишан бројот 4. Тој се наоѓа во ред каде индексот е еднаков на 3, а колоната е еднаква на 0. Со тој број, имаме означено дека постои ребро помеѓу темето означено со 3 и темето означено со 0, и дека тежината на тоа ребро е 4. Слично, од темето 3 постојат и две други ребра (со тежина 7), до темињата означени со индексите 2 и 4. Обидете се да ги откриете и другите ребра запишани во матрицата.

Пред да продолжиме понатаму, да забележиме дека, при решавањето на разни проблеми поврзани со графови, за означување на темињата ќе користиме броеви (од 0 до N-1, или пак од 1 до N – како ви е вам најлесно). Најверојатно, кога ќе решавате одреден проблем, истите и ќе ви бидат дадени на таков начин уште од почетокот. Сепак, доколку темињата ни се дадени на некој друг начин (на пример, со имиња – "Скопје", "Тетово", итн), можеме да искористиме мапа (map<string, int>, на пример), за означување на тоа кое име соодветствува на кој индекс, а потоа да продолжиме со решавање на проблемот како што е дадено погоре (со означување на темињата со помош на броеви). Едноставно, компјутерите работат најефикасно со помош на броеви, а и податочните структури кои се имплементирани многу поедноставно и побрзо работат на тој начин (наместо, на пример, со текстуални низи).

Вториот начин на кој што можеме да претставиме еден граф и ребрата во него е преку т.н. листи на соседство. Имено, замислете дека за секое теме во графот чуваме по една листа во која што ни се запишани темињата до кои постои ребро. На пример, за граф со 5 темиња, тоа може да изгледа вака:

Со листите на соседство дадени погоре, имаме обележано дека од темето означено со индекс 0 постојат ребра до темињата означени со 2 и 3. Слично, од темето означено со индекс 2, постојат ребра до темињата означени со 0 и 4, итн... Од темето означено со 1, не постојат ребра до ниту едно друго теме. Доколку работиме со тежински графови, наместо листите да ни содржат само броеви (како [2, 3]), тие може да се составени од пар од броеви, каде што првиот елемент ќе означува до кое теме покажува реброто, а вториот број неговата тежина – на пример, [ (2, 5), (3, 7) ], со што имаме претставено дека од тоа теме постои ребро до темето 2 (со тежина 5), и до темето 3 (со тежина 7). Се разбира, како што споменавме и во претходната дискусија, тежините можат да претставуваат должина, некоја друга мерка за проточност (на пример, колку литри вода може да се испраќаат по таа цевка во еден час, итн).

При пишувањето на програми, ќе забележите дека често ќе работиме со неориентирани графови (каде што ребрата немаат насока). Во таков случај, кога ќе обележуваме дека постои ребро од едно теме до друго (во листата), ќе запишеме и дека постои ребро од тоа друго теме до првото. На пример, ако го погледнете примерот даден погоре, ќе видите дека кај темето со индекс 0 имаме запишано дека од него постои ребро до темето 2, но и ако погледнеме во листата на соседство за темето со индекс 2, ќе видиме дека таму е запишано дека постои ребро до темето 0. На овој начин, алгоритмите кои ќе ги пишуваме ќе можат едноставно да ги одредуваат врските (за да видат до кои темиња постојат ребра).

За матрицата на соседство (првиот начин на претставување на граф за кој што зборувавме), ова се сведува на запишување на истата вредност во елементите на матрицата Gij и Gji (т.е., иста вредност во елементот со ред i и колона j, и елементот со ред j и колона i), бидејќи со елементот Gij означуваме дали постои ребро од темето i до темето j (или која е неговата тежина), а со елементот Gji означуваме дали постои ребро од темето j до темето i.

Пребарување на граф по длабочина

Постојат повеќе алгоритми кои ни овозможуваат да работиме со графови. Некои од нив се користат за откривање на темињата кои се достапни од некое друго теме (на пример, кои градови се достапни по патишта од Скопје), некои за откривање на најкраток пат помеѓу две темиња, итн.

Првиот алгоритам кој ќе го разгледаме е алгоритамот за пребарување на граф (прво) по длабочина (DFS – depth-first search). Идејата е едноставна – истражување на сите темиња преку движење во "длабочина" (т.е. се додека може да се оди во одредена насока), а кога веќе тоа не е возможно – истражување на други насоки (ребра) од истото теме. Кога и тоа веќе не е возможно (сме ги истражиле сите ребра од тековното теме), се враќаме наназад (рекурзивно) до темето преку кое сме дошле до сегашното, и потоа ги проверуваме останатите неистражени ребра. Ова е најлесно да се види преку пример, но и преку разгледување на код, бидејќи алгоритамот е мошне едноставен за имплементација. Засега, важно е да напоменеме и дека овој алгоритам може да се имплементира со помош на рекурзија, или со користење на податочната структура stack. Истиот можеме да го користиме кога сакаме да откриеме било кој пат помеѓу темиња (не најкраткиот), или кога сакаме ефикасно да ги посетиме сите темиња во еден граф (на пример, да изброиме колку ги има, во колку делови се тие поделени, итн).

Да ја разгледаме сега имплементацијата со помош на stack – која е делумно поефикасна и нема проблеми со надминување на мемориски лимит, бидејќи не користи рекурзија. Идејата е едноставна – одбираме едно теме од кое ќе почнеме да истражуваме, и истото го ставаме во stack. Од тука, кога ќе разгледуваме одредено теме од стекот (со циклус, едно по едно, почнувајќи од почетното), проверуваме дали тоа теме е можеби веќе посетено преку некој друг пат - а ако не е, тогаш означуваме дека тоа теме сме го посетиле и ги додаваме сите негови соседни темиња (темиња до кои има ребра). Да видиме како изгледа имплементацијата на овој алгоритам:

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

//grafot
vector<int> G[N];

void DFS(int start) 
{
     
     stack<int> stack;
     stack.push(start);
     
     int visited[N];
     memset(visited, 0, sizeof(visited));
     
     while(!stack.empty())
     {
          int node = stack.top();
          stack.pop();
          
          if (visited[node] == 0)
          {
               visited[node] = 1;
               
               for (auto next : G[node])
               {
                    if (visited[next] == 0)
                    {
                         stack.push(next);
                    }
               }
          }
     }
}

Бидејќи е ова прв алгоритам кој го разгледуваме од делот поврзан со графови, на него ќе посветиме малку повеќе време. Најпрвин, забележете дека за претставување на графот користиме листи на соседство (и тоа, N од нив, vector<int> G[N]). Следно, дефиницијата за тоа ја имаме напишано надвор од функцијата DFS(start). Ова е многу често при пишувањето на вакви програми, бидејќи многу е веројатно дека ќе имаме повеќе функции кои ќе ги повикуваме, па не сакаме да го наведуваме графот како параметар на секоја од нив. Се разбира, наместо N, треба да ставиме некој цел број (на пример, 100), кој ќе ни биде однапред даден при решавањето на разни проблеми (во практиката – веќе ќе знаеме колку градови има во некоја држава и слично; а за време на натпревари, бројот најчесто ќе ни биде даден во самата задача). Секој елемент од G соодветствува на листата на соседи на соодветното теме со тој индекс: G[0], G[1], G[2], итн. Во функцијата која што ја напишавме, при разгледувањето на секое теме "node" можеме да ги разгледаме сите негови соседни темиња користејќи for(auto next : G[node]).

Искористете колку време ви е потребно за да сфатите како и зошто ги користиме сите овие податоци: G ни служи за чување на листите на соседство, stack за чување на кои темиња треба да ги посетиме, а visited[] за обележување на оние темиња кои се веќе посетени (за да не ги посетуваме истите по повеќе пати или дури и бесконечно – на пример, замислете граф со циклус во него).

Да разгледаме сега и една конкретна задача каде што можеме да го искористиме алгоритамот за пребарување по длабочина DFS. Нека имаме задача каде што на почетокот ни е даден бројот на неколку држави (до 100), но и листа од ребра кои ќе означуваат дали постои гасовод помеѓу некои парови од нив (на пример, можно е да не постои доколку двете држави се наоѓаат на различен континент, итн). Сите гасоводи се двонасочни (во проблемот кој ние ќе го решаваме), па графот ќе го гледаме како да е неориентиран – т.е. како ребрата да немаат насока.

Сега, можно е да се случи овие држави да се поделат во неколку групи кои меѓусебно не се поврзани – на пример, ако дел од државите се наоѓаат на еден континент и постои гасоводен пат од секоја држава до секоја друга, и понатаму држави на друг континент каде постои гасовод помеѓу нив - но не и до државите од првиот континент. За ваквите изолирани групи ќе велиме дека се компоненти – всушност, "поврзана компонента" е множество од темиња кои се меѓусебно поврзани – т.е. постои пат помеѓу нив (преку едно или повеќе ребра). Наша задача ќе биде да откриеме од колку компоненти е составен овој граф.

Ова можеме да го решиме со едноставно користење на алгоритамот кој го напишавме погоре. Имено, да замислиме дека сме ја повикале функцијата DFS (дадена погоре) за првото теме. Оваа функција, користејќи го алгоритамот, ќе ги обележи (во низата visited) сите темиња кои се достапни со патишта. Ако, по завршување на алгоритамот, откриеме теме каде што visited[i] = 0 (кое не е посетено), ќе знаеме дека тоа припаѓа на друга компонента – па ќе ја повикаме функцијата DFS() да ги обележи и темињата достапни од таму. Слично, можеме со еден for циклус ова да го спроведеме за сите темиња. Резултатот од алгоритамот ќе биде тоа што функцијата DFS() ќе ја повикаме онолку пати колку што имаме изолирани компоненти во графот (бидејќи нема да ја повикаме за некое теме каде што веќе visited[i] = 1, и кое е веќе посетено). Единствена промена која што ќе треба да ја направиме во однос на алгоритамот даден погоре ќе биде да ја извлечеме низата visited[N] надвор од функцијата DFS(), бидејќи по нејзиното завршување ќе сакаме да знаеме кои темиња се веќе посетени и во функцијата main(). Да го разгледаме решението.

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

#include <iostream>
#include <vector>
#include <stack>
#include <cstring>
using namespace std;

const int MAX_N = 101;

vector<int> G[MAX_N];
int visited[MAX_N];

void DFS(int start) 
{
     
     stack<int> stack;
     stack.push(start);
     
     while(!stack.empty())
     {
          int node = stack.top();
          stack.pop();
          
          if (visited[node] == 0)
          {
               visited[node] = 1;
               
               for (auto next : G[node])
               {
                    if (visited[next] == 0)
                    {
                         stack.push(next);
                    }
               }
          }
     }
}



int main()
{
     int N, E;
     cout << "Number of countries: " << endl;
     cin >> N;
     
     cout << "Number of connections: " << endl;
     cin >> E;
     
     cout << "Enter the connections, one per line." << endl;
     for (int i=0; i<E; i++)
     {
          int country1, country2;
          cin >> country1 >> country2;
          
          G[country1].push_back(country2);
          G[country2].push_back(country1); //grafot e nenasocen
     }
     
     int numberOfComponents = 0;
     memset(visited, 0, sizeof(visited));
     
     for (int i=0; i<N; i++)
     {
          if (visited[i] == 0)
          {
               numberOfComponents++;
               DFS(i);
          }
     }
     
     cout << "Number of components: " << numberOfComponents;
     return 0;
}

Кога ќе имаме програми каде што нешто се бара на влез, пораките како "Number of countries: " ќе ги пишуваме на англиски. Барем јас (лично), при пишувањето на програми, се обидувам да пишувам имиња на променливи и пораки на англиски јазик, бидејќи наредбите во C++ (како if, else, while, итн) се такви, па (едноставно) делува поприродно. Сепак, коментарите, како и во сите програми досега, ќе бидат на македонски јазик - со цел полесно разбирање на самите предавања.

Пребарување на граф по широчина (BFS)

Следниот алгоритам за кој ќе зборуваме е алгоритамот за пребарување на граф по широчина (breadth-first search – BFS). Ова е всушност и омилениот алгоритам на авторот на овие предавања, истиот се користи за решавање на различни проблеми, и е исклучително едноставен за имплементација – се разбира, откако ќе се разбере како истиот функционира.

Пребарување по широчина се спроведува на начин што најпрвин го разгледуваме почетното теме, па потоа сите оние темиња кои се соседи (поврзани со ребро) со почетното теме (да ги наречеме "темиња од ниво 1", односно темиња до кои може да се стигне преку изминување на само 1 ребро од почетното теме), па потоа ги разгледуваме сите темиња кои се соседи (поврзани со ребро) со темињата од ниво 1 (да ги наречеме "темиња од ниво 2", ова се оние темиња до кои може да се дојде преку изминување на точно две ребра од почетното теме), итн. Забележете како, за разлика од алгоритамот за пребарување на граф по длабочина (DFS), тука темињата ги разгледуваме последователно во однос на нивното растојание (како број на ребра кои треба да се изминат) од почетното теме. Ова не важеше при пребарувањето по длабочина, каде што од почетното теме се движевме во одредена насока (на пример надесно, посетувајќи голем број на темиња на разна оддалеченост), пред воопшто да разгледавме некое друго соседно теме на почетното.

Имплементацијата на овој алгоритам изгледа вака:

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

//grafot
vector<int> G[N];

void BFS(int start) 
{
     
     int marked[N];
     memset(marked, 0, sizeof(marked));
     
     queue<int> queue;
     queue.push(start);
     marked[start] = 1;
     
     
     while(!queue.empty())
     {
          int node = queue.front();
          queue.pop();
          
          for (auto next : G[node])
          {
               if (marked[next] == 0)
               {
                    queue.push(next);
                    marked[next] = 1;
               }
          }
     }
}

Забележете дека ја користиме податочната структура queue<int> за чување на темињата кои треба да се посетат (оваа структура овозможува посетување на темињата по принципот прв влегува прв излегува, односно FIFO – first-in first-out). Дополнително, имаме и низа marked[], во која означуваме кои темиња ни се веќе посетени, за да не ги посетуваме истите по повеќе пати доколку во графот постојат циклуси, или пак истиот е ненасочен па можеме да се вратиме назад низ некое ребро.

И двата алгоритми кои ги разгледавме (DFS и BFS), во однос на имплементацијата која што ние ја напишавме, имаат временска сложеност O(V+E), каде V е бројот на темиња, a Е е бројот на ребра. При имплементација на овие алгоритми на друг начин (на пример, преку претставување на графот со матрица на соседство, или посетување на темињата по повеќе пати и слично), истите би имале и друга временска сложеност. Сепак, имплементациите кои што ние ги разгледавме се оние кои што се користат најчесто, и кои ќе ви бидат најмногу корисни при решавањето на разни задачи и проблеми.

Пред крајот на ова предавање, да пробаме да решиме и една задача со помош на алгоритамот за пребарување по широчина (BFS). Во следното предавање, ќе видиме и некои други примени на овој алгоритам – бидејќи истиот може да се користи за решавање на најразлични проблеми. Сега, да речеме дека ни е дадено едно дрво (како што споменавме погоре, дрво е неориентиран граф каде што било кои две темиња се поврзани со точно еден пат – односно, постои само еден начин да се стигне од едно теме до било кое друго). Дрвата, нормално, не содржат циклус и за истите знаеме дека бројот на ребра е за еден помал од бројот на темиња во дрвото (ако имаме 2 темиња, потребно е 1 ребро за истите да се поврзат така што постои само еден пат помеѓу нив; ако имаме 3 темиња, потребни се 2 ребра, итн).

Да пробаме да напишеме програма која што, почнувајќи од едно теме во дрвото (да го наречеме "корен"), ќе ги обележи нивоата на сите темиња - коренот е од ниво 0, сите негови директни соседи достапни преку едно ребро се од ниво 1, па сите нивни соседи се од ниво 2, итн. Овој проблем може едноставно да се реши со користење на алгоритамот за пребарување по широчина (BFS), бидејќи истиот ќе ги посети темињата по точниот редослед по кој ни е нам потребно (најпрвин коренот, па сите темиња од ниво 1, па сите темиња од ниво 2, итн). Единствено нешто на што треба да внимаваме е да го зачуваме нивото на секое теме како што го откриваме - кога сме кај коренот, да ги обележиме неговите соседи дека истите се од ниво 1, па кога сме кај темињата од ниво 1 да ги обележиме нивните непосетени соседи дека истите се од ниво 2, итн. Ова е реализирано со програмата дадена во продолжение.

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;

const int MAX_N = 101;

//grafot
vector<int> G[MAX_N];

//oznacuvanje na nivoto na sekoe teme
int level[MAX_N];


void BFS(int start) 
{
     
     int marked[MAX_N];
     memset(marked, 0, sizeof(marked));
     
     //sekogash e dobra ideja da gi inicijalizirame vrednostite vo niza (0)
     memset(level, 0, sizeof(level));
     
     queue<int> queue;
     queue.push(start);
     
     //korenot e vekje poseten, i istiot ima nivo 0
     marked[start] = 1;
     level[start] = 0;
     
     
     while(!queue.empty())
     {
          int node = queue.front();
          queue.pop();
          
          for (auto next : G[node])
          {
               if (marked[next] == 0)
               {
                    queue.push(next);
                    marked[next] = 1;
                    
                    //pronajdovme neposeteno teme
                    //postavi go negovoto nivo
                    level[next] = level[node] + 1;
               }
          }
     }
}






int main()
{
     int N;
     cout << "Number of vertices: " << endl;
     cin >> N;
     
     int E = N - 1; //brojot na rebra e N-1, bidejki grafot e drvo
     
     cout << "Enter the connections, one per line." << endl;
     for (int i=0; i<E; i++)
     {
          int v1, v2;
          cin >> v1 >> v2;
          
          G[v1].push_back(v2);
          G[v2].push_back(v1); //grafot e nenasocen
     }
     
     //pochnuvame od temeto 0 (kako toa da e koren na drvoto)
     //kaj nekoi problemi, koe teme e koren kje ni bide dadeno na vlez
     BFS(0);
     
     for (int i=0; i<N; i++)
     {
          cout << "Level of vertex " << i << " is equal to " << level[i] << endl;
     }
     
     return 0;
}

Забележете дека искористивме #include <queue> за да може да ја користиме податочната структура queue (како што за реализација на алгоритамот за пребарување по длабочина DFS искористивме #include <stack>). Доколку решите да ја тестирате оваа програма на вашиот компјутер, осигурајте се дека ребрата кои ќе ги внесете (поврзувањата помеѓу темињата) ќе претставуваат дрво – т.е. дека ќе постои пат помеѓу било кои две темиња. На пример, ако внесете N=5, тогаш можете да ги внесете следните ребра "0 1", "0 2", "0 3", "2 4". Како што можете да забележите, темето 0 е поврзано со темињата 1, 2 и 3, а постои и врска помеѓу темето 2 и темето 4. Бидејќи графот е неориентиран, постои пат помеѓу било кои две темиња од овој граф (на пример, постои пат од темето 0 до темето 2, постои пат од 0 до 4 преку 2, итн).

Во ова предавање, се запознавме со неколку основни поими од теоријата на графови, со начините на нивно претставување, и со алгоритмите за пребарување по длабочина (DFS) и по широчина (BFS). Во продолжение, ќе се запознаеме и со многу други алгоритми, и ќе видиме колку широка примена има всушност теоријата на графови. Голем дел од работите ќе ги повторуваме одново и одново (начинот на претставување, итн), па не се грижете ако постои некој дел кој не сте сигурни дека сте го сфатиле во целост.

Дозвола за користење: CC BY-NC 2.5 ©