Најкраток пат во лавиринт
Алгоритамот за пребарување на граф по широчина (BFS) е еден од најкористените алгоритми во теоријата на графови, и истиот може да се примени при решавањето на најразлични проблеми и задачи. Како што ќе видиме во продолжение, дел од тие проблеми можеби и не се иницијално дадени во вид на граф, но истите можат да се претворат во проблеми од теоријата на графови со цел нивно поефикасно решавање.
Во ова предавање, најпрвин ќе разгледаме како алгоритамот BFS може да се примени за пронаоѓање на најкраток пат во лавиринт, бидејќи тие проблеми често се среќаваат на натпреварите по информатика, роботика, и слично. Дополнително, ќе разгледаме и една варијација на проблемот, од каде што едноставно ќе може да се забележи како, со едноставни и кратки промени, може да се решаваат најразлични проблеми со лавиринти (најкраток пат помеѓу две локации, најкраток пат ако најпрвин треба да поминеме низ трета локација и да земеме некој важен предмет, итн).
Понатаму, ќе споменеме и неколку проблеми кои иницијално не ни се дадени во форма на граф, но кои може да се претворат во проблеми каде што може да се искористат алгоритми од теоријата на графови.
Пронаоѓање на најкраток пат во лавиринт
Најпрвин, да го дефинираме проблемот кој сакаме да го решиме. Да замислиме дека ни е дадена матрица како што е прикажано на сликата подолу, која што содржи некои полиња (обележени со бела боја) низ кои можеме да се движиме, и други полиња (обележени со сива боја) низ кои не можеме да се движиме (да ги наречеме пречки). Доколку ни се дадени две локации во матрицата (почетна и крајна), дали можеме да напишеме програма која што ќе го пронајде најкраткиот пат од почетната до крајната локација (како број на движења помеѓу соседни полиња), без да застануваме на оние полиња кои содржат пречки? Од десната страна на сликата, прикажан ни е најкраткиот пат помеѓу почетното поле (S) и крајното поле (E).
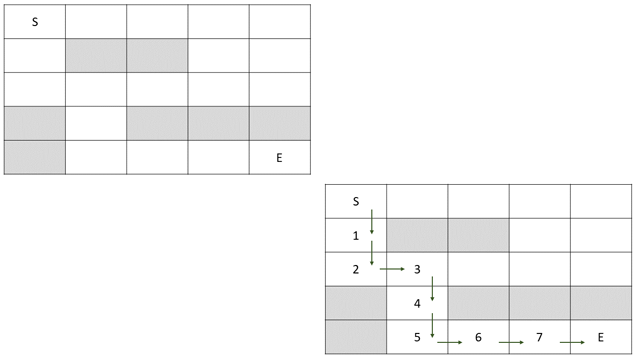
Овој проблем можеме да го решиме со помош на алгоритамот за пребарување на граф по широчина (BFS). Имено, како што споменавме во претходното предавање, овој алгоритам ги разгледува темињата (во нашиот случај, тоа се полињата во матрицата), по редослед на нивната оддалеченост од почетното теме. Ако ги означуваме темињата со нивната оддалеченост како што ги изминуваме истите (колку полиња сме требале да поминеме за да стигнеме до таму), бројот кој ќе ни биде запишан во секое поле точно ќе соодветствува на бараното минимално растојание за стигнување до таа локација. Со други зборови, ако го споредуваме решавањето на овој проблем со примерот кој го дадовме во претходното предавање, каде што почетното теме при решавањето го означивме дека е од ниво 0, па потоа сите темиња достапни преку едно ребро како да се од ниво 1, па потоа сите темиња достапни преку темињата од ниво 1 преку едно ребро како да се од ниво 2, итн; тогаш нивото кое го имаме запишано за секое теме (0, 1, 2, ...) е точно оддалеченоста (во вид на број на полиња кои треба да се поминат) за стигнување до тоа теме.
Пред да разгледаме како изгледа имплементацијата на ова решение, да забележиме уште неколку работи. Имено, за разлика од решавањето на претходните проблеми, тука нема потреба да ги чуваме врските на графот ниту како матрица на соседство, ниту со листи на соседство (иако можеме, ако сакаме). Имено, кога ќе разгледуваме одредено теме, веднаш знаеме кои се темињата достапни преку него: оние кои се наоѓаат веднаш до него во матрицата. Со други зборови, нема потреба однапред да дефинираме листи на соседство G[i], каде таа листа ги содржи ребрата од темето i, и кои темиња се достапни преку нив. Напротив, ако моментно се наоѓаме кај темето (ред 3, колона 4), на пример, тогаш достапни следни полиња се она над него (ред 2, колона 4), она под него (ред 4, колона 4), она лево од него (ред 3, колона 3), итн. Зависно од тоа дали ќе дозволуваме дијагонално движење во матрицата, или само хоризонтално и вертикално, достапни ќе ни бидат или 8 темиња (ако е дозволено дијагонално движење), или само 4. Ова ќе го видиме во продолжение.
Последната забелешка која што сакаме да ја споменеме е дека често се користи само една матрица за чување на сите податоци за лавиринтот. Имено, при читање на податоците, можеме да користиме матрица со соодветна големина за претставување на лавиринтот, и притоа да користиме одредени броеви за обележување на соодветните полиња (да го означиме почетното поле со 0, да ги означиме пречките со -1, а за секое останато поле да го чуваме растојанието до него – 1, 2, 3, итн). Слично, нема потреба да имаме друга низа каде ќе чуваме дали едно теме ни е веќе посетено или не (како што имавме кај претходното разгледување на алгоритамот BFS), бидејќи овој податок можеме да го прочитаме од самата матрица. Сепак, доколку сакаме (така ни е полесно за размислување), можеме да користиме и таква низа.
Да ја разгледаме оваа имплементација во програмскиот јазик C++:
Програма 16.1
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <iostream>
#include <queue>
using namespace std;
//slednite promenlivi go definiraat lavirintot.
//koristime 999999 (nekoja golema vrednost)
//za oznachuvanje na polinjata za koi (seushte) ne sme
//go presmetale rastojanieto od pochetokot
int rows = 5, cols = 5;
int labyrinth[5][5] =
{
{ 0, 999999, 999999, 999999, 999999 },
{ 999999, -1, -1, 999999, 999999 },
{ 999999, 999999, 999999, 999999, 999999 },
{ -1, 999999, -1, -1, -1 },
{ -1, 999999, 999999, 999999, 999999 }
};
//pochetnata i krajnata pozicija najchesto kje ni bidat dadeni odnapred
//vo ovoj primer, (0, 0) e pochetokot, a (4, 4) e krajot, t.e. ako ja vidime
//matricata pogore, barame rastojanie od temeto gore-levo do ona dolu-desno
int start_row = 0, start_col = 0;
int end_row = 4, end_col = 4;
//proveri dali odredeno pole e validno
bool valid_move(pair<int, int> next)
{
//validno ako sme vo matricata (ne mozhe da izlezeme nadvor), i nema prechka
return (next.first >= 0 && next.first < rows
&& next.second >= 0 && next.second < cols
&& labyrinth[next.first][next.second] != -1);
}
vector<pair<int, int> > possible_moves(pair<int, int> node)
{
vector<pair<int, int> > moves;
moves.push_back({node.first, node.second - 1}); //odi levo
moves.push_back({node.first, node.second + 1}); //odi desno
moves.push_back({node.first - 1, node.second}); //odi nagore
moves.push_back({node.first + 1, node.second}); //odi nadolu
//ako se dozvoleni i dijagonalni dvizenja
//moves.push_back({node.first - 1, node.second - 1});
//moves.push_back({node.first - 1, node.second + 1});
//moves.push_back({node.first + 1, node.second - 1});
//moves.push_back({node.first + 1, node.second + 1});
return moves;
}
int BFS()
{
queue<pair<int, int> > queue;
queue.push({start_row, start_col});
while (!queue.empty())
{
auto node = queue.front();
queue.pop();
vector<pair<int, int> > moves = possible_moves(node);
for (auto next : moves)
{
if (valid_move(next))
{
if (labyrinth[next.first][next.second] == 999999)
{
//ova e neposeteno pole
queue.push(next);
int distance = labyrinth[node.first][node.second] + 1;
labyrinth[next.first][next.second] = distance;
}
}
}
}
}
int main()
{
BFS();
int distance = labyrinth[end_row][end_col];
cout << distance << endl;
}
Забележете дека го користиме истиот алгоритам за пребарување на граф по широчина (BFS) како и претходно – користејќи queue, разгледувајќи ги темињата едно по друго, итн. Кога ќе откриеме ново непосетено теме, го забележуваме неговото растојание од почетокот - тоа е за 1 поголемо од растојанието на претходното теме (она преку кое сме го откриле новото).
Кога разгледуваме едно поле и сакаме да дознаеме кои се неговите соседи (до кои можеме да дојдеме со еден чекор), ја користиме функцијата possible_moves() за да ги создадеме истите во самиот тој момент. Се разбира, потребно е и да провериме дали создадените соседни полиња се воопшто валидни – дали се истите во матрицата или можеби надвор од неа (на пример, полето [-1, 3] e невалидно, бидејќи редот -1 не постои), но и да внимаваме да не стапнеме на поле на кое има пречка (обележано со -1 во матрицата).
Најчесто, при решавање на вакви проблеми, големината на матрицата и елементите во неа ќе ни бидат дадени како влезен податок, наместо да се директно запишани во програмата. Во примерот даден погоре, овие податоци беа дел од изворниот код за полесно разбирање на истиот. Се разбира, потребни се само минимални промени за нивно читање од стандарден влез или датотека (cin >> rows >> cols, cin >> start_row >> start_col, итн).
Временската сложеност на алгоритамот даден погоре е O(V), бидејќи сложеноста на алгоритамот за пребарување по широчина BFS е O(V+E), а бројот на ребра во нашиот случај е директно зависен од бројот на темиња – најчесто x4 доколку не дозволуваме дијагонални движења (или x8, доколку такви движења се дозволени). Бидејќи кај анализирањето на временската сложеност ги исфрламе сите константи (во случајов, V+4V = 5V), добиваме дека алгоритамот има линеарна временска сложеност O(V), во однос на бројот на темиња. Инаку, доколку сакаме, можеме да одиме и понатаму со анализата, и да видиме дека бројот на темиња V е еднаков на големината на матрицата (бројот на редови * бројот на колони), па да запишеме и дека сложеноста е O(R * C).
Да се обидеме сега да решиме еден многу посложен проблем. Иако истиот е можеби надвор од опсегот (тежината) на овие предавања, и е нешто што би можело да се појави на некоја олимпијада по информатика, сепак сметам дека проблемот е интересен и ќе придонесе за сфаќање на тоа колку се моќни алгоритмите кои ги разгледуваме и како истите можат да се применат при решавање на разни проблеми. Ќе видиме како со мала промена на програмата дадена погоре, можеме да решиме многу посложен проблем од оној класичниот на пронаоѓање на најкраток пат во лавиринт помеѓу две точки. Дополнително, програмата која што ќе ја напишеме овој пат ќе го прочита изгледот на лавиринтот од влез, наместо истиот да биде запишан директно во програмскиот код.
Проблемот е следен: нека ни е даден изглед на лавиринт, каде ни е познато кои полиња претставуваат пречки, и нека ни е дадено почетното поле и крајното поле (значи, исто како и кај класичниот проблем кој го решававме). Но, овој пат, да замислиме дека постои и некое трето поле низ кое треба да поминеме пред да стигнеме до крајното поле (на пример, нека таму се наоѓа некој предмет, батерија или слично кое што треба да го земеме). Како можеме да го решиме ова, и да пресметаме со колку најмалку чекори можеме да дојдеме од почетното поле, па преку третото поле, се до крајното?
Интересно, овој проблем (и слични на него, можеби каде што треба да поминеме низ повеќе точки итн), можат да се решат со мала модификација на основниот алгоритам кој го искористивме. Ако се навратите на тоа решение, ќе забележите дека во матрицата labyrinth[][], го чувавме растојанието (како број) до тоа поле (нормално, со исклучок на пречките, кои ги означивме со -1). Ова значи дека, кога разгледуваме некое поле од матрицата labyrinth[r][c], очекуваме таму да се наоѓа вредност која ни кажува со колку најмалку потези може да се стигне до полето [r][c], тргнувајќи од почетното поле во лавиринтот. Ако таму е запишан бројот 7, на пример, тоа значи дека се потребни 7 чекори за да стигнеме до тоа поле.
Но, кај новиот проблем кој што го разгледуваме, не ни е доволно да имаме матрица со само две димензии labyrinth[r][c], бидејќи кога имаме запишано некој број таму (на пример, 7) не знаеме дали претходно сме поминале низ третото поле (да го земеме бараниот предмет, батерија или слично), или не сме поминале низ него пред доаѓањето до полето [r][c]. Решението на овој проблем е едноставно – што ако во матрицата додадеме нова димензија, која ќе ни означува дали сме поминале низ полето или не? На пример, labyrinth[r][c][0] може да ни означува дека не сме поминале низ полето сеуште, додека labyrinth[r][c][1] може да ни означува дека веќе сме поминале низ полето. Тогаш, доколку крајното поле се наоѓа на локацијата (er, ec), бараното решение ќе биде вредноста запишана во labyrinth[er][ec][1], бидејќи на тоа место во матрицата се наоѓа најкраткото растојанието до (er, ec) кога веќе сме поминале и низ третото поле (labyrinth[er][ec][0] е најкраткото растојание до таа локација, ако сеуште не сме поминале низ третото поле).
Во претходната програма, искористивме pair<int, int> за чување на темињата кои сеуште не сме ги посетиле. Бидејќи сега во податочната структура queue треба да запишуваме по три броеви, ќе креираме нова структура на податоци state (со два броја за локацијата, и еден за тоа дали третото поле е веќе посетено или не – нека го именуваме тој трет број took_object – т.е. означуваме дали сме го земале бараниот предмет или не). Кога ќе преоѓаме од некое поле на друго соседно поле, вредноста на took_object ќе биде еднаква на онаа вредност која била запишана во претходната состојба (дали предметот е земен пред да прејдеме на новото поле) или ќе запишеме во истата "1" (дека предметот е земен) ако се поместиме на локацијата на третото поле (каде што се наоѓа предметот). Ова е многу логично - предметот или сме го земале досега или не сме го земале, но доколку не сме го земале а дојдеме до полето на кое што тој предмет се наоѓа, тогаш нормално е дека истиот ќе го земеме во наш посед. Реализацијата на се што зборувавме погоре, напишана во програмскиот јазик C++, е дадена во продолжение.
Програма 16.2
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <iostream>
#include <queue>
using namespace std;
const int MAX_RC = 101;
//kje gi prochitame ovie vrednosti vo main()
int rows, cols;
int labyrinth[MAX_RC][MAX_RC][2];
int start_row, start_col;
int object_row, object_col;
int end_row, end_col;
struct state
{
int row, col, took_object;
};
//proveri dali poleto e validno za poseta
bool valid_move(state next)
{
return (next.row >= 0 && next.row < rows
&& next.col >= 0 && next.col < cols
&& labyrinth[next.row][next.col][next.took_object] != -1);
}
state build_next_move(int row, int col, int previous_took_object)
{
state move;
move.row = row;
move.col = col;
move.took_object = previous_took_object;
if (previous_took_object == 0 && move.row == object_row && move.col == object_col)
{
//go nemavme predmetot prethodno, no, vo ovoj poteg, kje zastaneme
//na toa pole, pa sega go imame i predmetot
move.took_object = 1;
}
return move;
}
vector<state> possible_moves(state node)
{
vector<state> moves;
moves.push_back(build_next_move(node.row, node.col - 1, node.took_object)); //odi levo
moves.push_back(build_next_move(node.row, node.col + 1, node.took_object)); //odi desno
moves.push_back(build_next_move(node.row - 1, node.col, node.took_object)); //odi nagore
moves.push_back(build_next_move(node.row + 1, node.col, node.took_object)); //odi nadolu
return moves;
}
int BFS()
{
queue<state> queue;
state initial;
initial.row = start_row;
initial.col = start_col;
initial.took_object = 0; //go nemame predmetot na pochetokot (ne sme stapnale na tretoto pole)
queue.push(initial);
while (!queue.empty())
{
auto node = queue.front();
queue.pop();
vector<state> moves = possible_moves(node);
for (auto next : moves)
{
if (valid_move(next))
{
if (labyrinth[next.row][next.col][next.took_object] == 999999)
{
queue.push(next);
int distance = labyrinth[node.row][node.col][node.took_object] + 1;
labyrinth[next.row][next.col][next.took_object] = distance;
}
}
}
}
}
int main()
{
cout << "Enter the dimensions of the labyrinth: " << endl;
cin >> rows >> cols;
cout << "Enter the start location: " << endl;
cin >> start_row >> start_col;
cout << "Enter the location of the object: " << endl;
cin >> object_row >> object_col;
cout << "Enter the end location: " << endl;
cin >> end_row >> end_col;
//inicijaliziraj ja matricata so koja e pretstaven lavirintot
for (int r=0; r < rows; r++)
{
for (int c=0; c < cols; c++)
{
labyrinth[r][c][0] = 999999;
labyrinth[r][c][1] = 999999;
if (r == start_row && c == start_col)
{
//pochetnoto pole go oznachuvame so 0
labyrinth[r][c][0] = 0;
}
}
}
int obstacles;
cout << "How many obstacles are in the labyrinth: " << endl;
cin >> obstacles;
cout << "Enter the locations of the obstacles, one per line." << endl;
for (int i=0; i < obstacles; i++)
{
int obstacle_row, obstacle_col;
cin >> obstacle_row >> obstacle_col;
labyrinth[obstacle_row][obstacle_col][0] = -1;
labyrinth[obstacle_row][obstacle_col][1] = -1;
}
BFS();
int distance = labyrinth[end_row][end_col][1];
cout << distance << endl;
}
Постои и друго решение на проблемот даден погоре, каде што наместо да имаме матрица со три димензии, можеме да го искористиме алгоритамот за пребарување по широчина (BFS) два пати, притоа собирајќи ги добиените вредности – еднаш за наоѓање на најкраток пат од почетното поле до третото поле, а потоа и за наоѓање на најкраток пат од третото поле до крајното поле во лавиринтот (едноставно, во тој случај, ќе го извршевме алгоритамот поставувајќи дека почетокот е во третото поле и така ќе дојдевме до бараната вредност). Сепак, решението што го разгледавме погоре е многу помоќно, бидејќи истото може да се искористи и за решавање на многу други проблеми – чувајќи ги, како димензија/димензии во матрицата, бараните параметри од кои ни зависи решението (кој предмет/и треба да ги земеме, дали сме искористиле или не некој билет за поминување низ пречка/и, итн).
Решавање на други проблеми
Алгоритамот за пребарување по широчина (BFS) може да се искористи и за решавање на многу други проблеми - дури и онакви кои иницијално не ни се претставени во форма на граф. Една таква група на проблеми се оние каде што ни е дадено множество од можни елементи или состојби (локации, цели броеви, некакви топчиња, итн), и листа на операции кои што можат да се извршат за префрлување од една состојба во друга. Замислете сега дека од нас се бара да пресметаме со колку најмалку операции може да дојдеме од некоја почетна состојба до некоја крајна состојба. Во вакви ситуации, можеме да го претставиме проблемот со помош на граф, и да го искористиме алгоритамот за пребарување по широчина (BFS) за негово решавање.
На пример, нека ни е даден некој почетен број (на пример, N=10), некој краен број до кој треба да стигнеме (на пример, R=63) и листа на операции кои што можеме да ги извршиме врз даден број (нека биде тоа "множење со 2", "множење со 3", и "додавање на бројот 1, односно собирање со 1"). Од бројот N=10 до бројот R=63, во овој случај, можеме да стигнеме со 3 операции: прво множење со 2 за да стигнеме до 10*2=20, па додавање на 1 за да стигнеме до 20+1=21, па множење со 3 за да стигнеме до 21*3=63. Но, како да напишеме алгоритам за нашиот компјутер да може да го реши овој проблем за било кои броеви N и R?
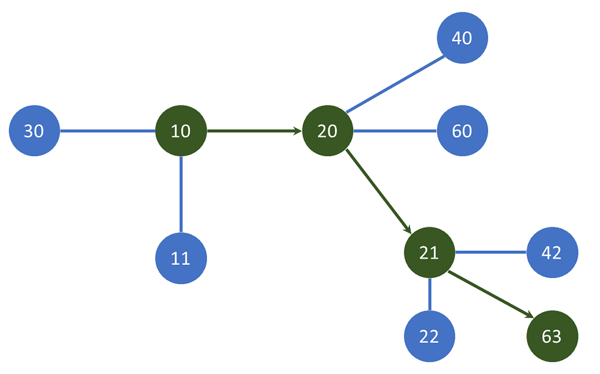
Решението е едноставно, и се сведува на следната идеја: броевите можеме да ги гледаме како темиња на еден граф, а операциите како ребра преку кои можеме да дојдеме од едно теме (на пример, 10) до друго (30). Бидејќи алгоритамот за пребарување по широчина ги разгледува темињата по нивната оддалеченост од почетното теме (како што видовме кога го решававме проблемот на пронаоѓање на најкраток пат во лавиринт), истиот ќе дојде до целта со најмал број на поминати ребра (што во нашиот случај означува најмал број на операции). Сепак, запаметете дека алгоритамот BFS функционира само во ситуации кога сите ребра се еднакви по тежина/должина – па така, на пример, кај лавиринтот ги разгледуваме сите соседни темиња како да се на оддалеченост 1 (еден чекор). Овој алгоритам нема да дојде до точниот резултат ако чекорите (или во тековниот случај, операциите за движење од еден број до друг) се вреднуваат различно – т.е. мора да се бара од нас да го најдеме најмалиот број на операции каде секоја од нив се брои како 1. Едноставно, алгоритамот BFS ги разгледува соседите на едно теме како еднакви (без да им дава предност на оние каде ребрата имаат помала тежина, или операцијата има помала цена, итн). Запаметете го овој факт! Истиот ќе го повториме и во следното предавање, каде што ќе разгледаме алгоритам кој што точно го решава проблемот каде што ребрата имаат различна тежина, и сакаме да го искористиме тој факт при решавање на соодветниот проблем.
Да се вратиме сега на алгоритамот за пребарување по широчина, бидејќи истиот има голема примена кај проблеми како оној за определување на бараниот најмал број на операции (бидејќи ребрата во тој граф немаат тежина, или може да ги гледаме истите како сите да имаат еднаква тежина 1). Како што рековме, главната потешкотија е да забележиме дека проблемот можеме да го претставиме со помош на граф. Потоа, единствено треба да го искористиме алгоритамот BFS. Како и кај решавањето на лавиринт, нема потреба да ги претставуваме сите ребра на почетокот (со матрица или листи на соседство), туку ребрата и следните темиња за разгледување можеме да ги создадеме при разгледувањето на секој од броевите од редот (на пример, ако бројот кој моментно го разгледуваме е 10, следни за разгледување како темиња се броевите 10*2, 10*3 и 10+1, бидејќи дозволени операции во нашиот случај се множење со 2, множење со 3, и додавање на бројот 1). Да видиме како изгледа програмскиот код за решавање на овој проблем:
Програма 16.3
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
vector<int> possible_operations(int node)
{
vector<int> moves;
moves.push_back(node*2);
moves.push_back(node*3);
moves.push_back(node+1);
return moves;
}
int BFS(int N, int R)
{
queue<int> queue;
int operations[R + 1];
memset(operations, 127, sizeof(operations)); //nekoj golem broj
queue.push(N);
operations[N] = 0; //trebaat 0 operacii za da se stigne do N (pochetok)
while (!queue.empty())
{
auto node = queue.front();
queue.pop();
if (node == R)
{
//go najdovme odgovorot
break;
}
vector<int> moves = possible_operations(node);
for (auto next : moves)
{
if (next <= R) //ne razgleduvame broevi pogolemi od R
{
if (operations[next] > operations[node] + 1)
{
//mozhe da odime od node do next so 1 operacija
operations[next] = operations[node] + 1;
queue.push(next);
}
}
}
}
return operations[R];
}
int main()
{
int N, R;
cout << "Please enter N and R (make sure R>N): " << endl;
cin >> N >> R;
int minOperations = BFS(N, R);
cout << minOperations << endl;
return 0;
}
Интересен и краток програмски код, а истиот ни покажува како да го искористиме алгоритамот за пребарување по широчина за решавање на најразлични проблеми. На пример, замислете дека сте вработени во компанија која работи на софтвер за решавање на математички проблеми, и сакате да напишете програма која што ќе решава задачи со најмал број на операции. Поконкретно, ако во софтверот ги внесеме операциите кои може да се прават кај една равенка, тој софтвер би решавал најразлични равенки исклучително брзо – и истиот може да се користи од ученици за проверка на нивните домашни задачи, итн. Едноставно, темињата ќе ни ја претставуваат равенката до која сме стигнале, а ребрата (операциите) како можеме да прејдеме од една равенка до друга, како што е прикажано подолу.
2x + 3 = 5 – 6 (теме 1, почеток)
2x = 5 – 6 – 3 (теме 2, дојдено преку теме 1, со одземање на 3 од двете страни)
2x = -4 (теме 3, дојдено од теме 2, со пресметка на вредноста од десната страна)
x = -2 (теме 4, дојдено преку теме 3, со делење на двете страни со 2)
Во ова предавање, разгледавме неколку примени на теоријата на графови, каде се фокусиравме на алгоритамот за пребарување по широчина (BFS). Истиот може да се користи за решавање на најразлични проблеми – истражување на врските во еден граф, пронаоѓање на најкраток пат во лавиринт (каде сите ребра, односно движења од едно теме до неговите соседни темиња, имаат иста должина 1), пронаоѓање на најмалиот број на операции за доаѓање од една состојба до друга, итн. Запаметете дека алгоритамот се имплементира едноставно – со користење на податочната структура ред (queue), и дека, како и кај другите алгоритми од теоријата на графови кои ќе ги разгледаме, многу е важно да имаме некоја низа (или мапа), каде што ќе забележиме кои темиња ни се веќе посетени, или која е далечината до нив (доколку тоа се бара во задачата). Ова е од исклучително значење кај алгоритмите од теоријата на графови, бидејќи често постои начин да се патува по обратен редослед (од едно теме до друго, и обратно), па не сакаме да западнеме во ситуација каде што разгледуваме едни исти темиња по бесконечен број на пати.




