Најкраток пат. Минимално опфаќачко дрво
Како што споменавме и претходно, многу различни проблеми можат да се решат со помош на теоријата на графови, и разните алгоритми кои спаѓаат во таа област. Еден од најкласичните проблеми кои наоѓаат разна примена е пронаоѓањето на најкраток пат во граф (на пример, пат помеѓу два града, каде со графот ги имаме претставено градовите како темиња, а патиштата помеѓу нив како ребра).
Во ова предавање, ќе го разгледаме алгоритамот за пронаоѓање на најкраток пат во граф Dijkstra, кој може да се примени на графови каде што тежините на ребрата (на пример, должините на патиштата) се ненегативни броеви (броеви поголеми или еднакви на 0) - што е често случај. Алгоритамот, почнувајќи од одредено теме (да го наречеме "извор"), ги наоѓа растојанијата од тоа теме до сите останати темиња во графот.
Во продолжение, бидејќи е многу сличен на алгоритамот Dijkstra (бара промена на само две линии од програмскиот код), ќе зборуваме и за еден сосема друг проблем – откривање на минимално опфаќачко дрво.
Откривање на најкраток пат во граф
При разгледувањето на алгоритамот за пребарување по широчина (BFS), споменавме дека истиот може да открива најкраток пат помеѓу две темиња, ако сите ребра во графот имаат иста тежина. Едноставно, кога сите ребра имаат иста тежина, тогаш најкраткиот пат точно зависи од бројот на ребра кои треба да се поминат за доаѓање од едното теме до другото. На пример, при разгледувањето на проблемот со наоѓање на пат во лавиринт, ако двете темиња се наоѓаа едно до друго, тогаш растојанието помеѓу нив е 1, бидејќи треба да се помине едно ребро (врската помеѓу тие темиња), итн.
Но, при разгледувањето на разни проблеми, често се среќаваме со ситуации каде што ребрата во графот имаат различна тежина. На пример, ако разгледуваме патна мрежа во одредена држава, и темињата ни ги означуваат градовите во државата, тогаш кај ребро кое што го означува патот од Скопје до Куманово, на пример, може да запишеме тежина 40, означувајќи дека растојанието помеѓу тие градови е 40 километри. За други два града, тежината ќе биде некој друг број (на пример, 27). Забележете дека, при коментирањето на графови, стандардно го користиме терминот тежина при дискусија за ребрата во графот, но таа тежина може да претставува било кој број кој ќе ни биде од интерес при анализата на графот - на пример, должина на пат.
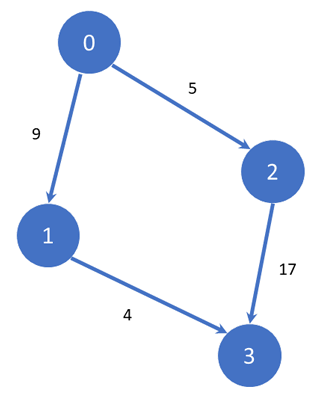
Алгоритамот Dijkstra се користи за пресметка на најкраткиот пат во граф помеѓу едно почетно теме (извор), и сите останати темиња во графот. На пример, ако зборуваме за патна инфраструктура, може да одбереме дека изворот е градот Скопје, и алгоритамот Dijkstra ќе ни го пресмета најкраткиот пат (растојанието) од тој град до сите останати градови во државата. Единствено ограничување е фактот што сите ребра мора да имаат тежина која не е негативен број (на пример, -1912 е погрешно). Ова е случај кај скоро сите проблеми кои се разгледуваат, па алгоритамот Dijkstra наоѓа широка примена во повеќе области и задачи.
Забележете дека во наредното предавање ќе зборуваме и за два други алгоритми. Едниот од нив (Bellman-Ford) работи на сличен начин како и алгоритамот Dijkstra, но истиот функционира на правилен начин и кога ребрата имаат тежини кои се негативни броеви (за сметка на ова, тој има поголема временска сложеност, и работи побавно). Вториот алгоритам кој ќе го разгледаме се нарекува Floyd-Warshall, и истиот се користи кога сакаме да го пресметаме растојанието од сите темиња до сите останати темиња (кога немаме едно почетно теме како извор). И двата алгоритми се едноставни за имплементација. Сепак, забележете дека она за што ќе зборуваме во ова предавање (алгоритамот Dijkstra) се користи многу почесто, и истиот е исклучително важен – како што е всушност и теоријата на графови во целост, која наоѓа широка примена насекаде.
Имплементацијата на алгоритамот Dijkstra е многу слична на алгоритамот за пребарување на граф по широчина BFS. Главната разлика помеѓу нив е што кај алгоритамот Dijkstra се користи приоритетен ред (priority_queue) наместо ред. Ова е важно кај овој алгоритам бидејќи сакаме да ги разгледуваме темињата според нивното вкупно растојание од почетното теме (изворот), односно според збирот на тежините на ребрата низ кои треба да се помине за да се стигне до таму. Кај алгоритамот BFS можевме да користиме едноставен ред (queue), бидејќи сите ребра имаа иста тежина. Од кога ќе го забележиме овој факт, алгоритамот е исклучително едноставен за имплементација.
Пред да го видиме изворниот код за овој алгоритам, да напоменеме еден важен дел кој ќе ни помогне полесно да го разбереме истиот. Имено, бидејќи ќе користиме приоритетен ред, важно ќе ни биде да ги разгледуваме елементите во него според нивното растојание од изворот по растечки редослед (прво да ги разгледуваме оние кои се најблиску до изворот), слично како и кај алгоритамот BFS. Бидејќи, кога ќе гледаме во еден елемент од приоритетниот ред, ќе ни биде важно колкаво е растојанието до тоа теме но и за кое теме всушност се работи, можеме да користиме pair<int, int> за чување и на двете вредности. Кога системот споредува два вакви пара, тие прво се споредуваат по првата вредност во парот, па таму ќе го чуваме растојанието – како pq.push({ distance, city }). Сега, кога разгледуваме еден елемент од приоритетниот ред, во e.first ќе го имаме растојанието, а во e.second темето (во случајот на нашиот проблем, градот кој го разгледуваме во моментот). Но, она што е многу важно е дека приоритетниот ред најпрвин ќе ни ги дава оние елементи каде што растојанието е најголемо (така функционира priority_queue), што очигледно не сакаме. Поради тоа, при имплементацијата на алгоритамот Dijkstra, кога ќе додаваме нов елемент, ќе ја додаваме вредноста pq.push({ -distance, city }). Забележете како напишавме (-distance) наместо само (distance). Едноставно, наместо да додаваме растојанија како 3, 9, 17, ќе додаваме -3, -9, -17, па кога од приоритетниот ред ќе разгледуваме елементи, ќе ги добиваме во редоследот -3, -9, -17, односно повторно од најголем кон најмал (бидејќи така функционира приоритетниот ред), но сега можеме уште еднаш (по вадењето на елементот) да искористиме минус за да го поништиме претходниот, и да го добиеме тековното растојание (-(-3)) = 3, итн. Малку комплицирано за да се сфати на почеток, но од кога ќе го сфатиме тој дел, алгоритамот е исклучително едноставен и краток за пишување.
Програма 17.1
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int MAX_N = 101;
int N, E;
vector<pair<int, int> > G[MAX_N];
vector<int> dijkstra(int start)
{
vector<int> distance;
distance.resize(MAX_N);
for (int i=0; i<MAX_N; i++)
{
distance[i] = 1000000000; //nekoj golem broj
}
priority_queue<pair<int, int> > pq;
distance[start] = 0;
pq.push({0, start});
int visited[MAX_N];
memset(visited, 0, sizeof(visited));
while (!pq.empty())
{
pair<int, int> state = pq.top();
pq.pop();
int city = state.second, distance_to_city = -state.first;
if (visited[city] == 0)
{
visited[city] = 1;
for (auto edge : G[city])
{
int next = edge.first, distance_between_cities = edge.second;
if (distance[next] > distance[city] + distance_between_cities)
{
distance[next] = distance[city] + distance_between_cities;
pq.push({ -distance[next], next });
}
}
}
}
return distance;
}
int main()
{
cout << "Number of cities: " << endl;
cin >> N;
cout << "Number of edges: " << endl;
cin >> E;
cout << "Enter the edges (from, to, weight)." << endl;
for (int i=0; i<E; i++)
{
int from, to, weight;
cin >> from >> to >> weight;
G[from].push_back({to, weight});
}
int start;
cout << "Start city: " << endl;
cin >> start;
vector<int> distance = dijkstra(start);
for (int i=0; i<N; i++)
{
cout << "min distance to " << i << " is: " << distance[i] << endl;
}
return 0;
}
Забележете ја употребата на дополнителната низа visited, како и проверката (visited[city] == 0), бидејќи таа е исклучително важна за постигнување на оптималната временска сложеност. Имено, при извршувањето на овој алгоритам, можно е да постојат повеќе начини за да се стигне од еден град до некој друг – дури и онакви каде што можеби постои пат помеѓу два града каде што треба да се поминат две ребра (да кажеме споредни патишта), но постои пократок пат (како вкупен број на километри) каде што се поминуваат три автопати. Значи, најкраткото растојание може да поминува низ повеќе ребра (во случајов, 3) отколку некој друг начин за патување кој што можеби е подолг бидејќи патот е неквалитетен, поминува околу планина наместо низ тунел, итн.... Поради тоа, важно е, како што е направено со проверката (visited[city] == 0), од кога ќе го откриеме најкраткото растојание до некој град, да не ги разгледуваме другите можни патишта кои водат до таму, бидејќи тие не можат да го подобрат резултатот – едноставно, користевме приоритетен ред, па знаеме дека штом за некој град веќе сме разгледале пократко растојание, нема потреба да разгледуваме некои други патишта со поголемо растојание. Јасно, бидејќи сите ребра имаат ненегативни тежини (што беше услов за користење на алгоритамот Dijkstra), знаеме дека такво нешто не може да се случи. Временската сложеност на овој алгоритам е O(E * log(V)), каде E е бројот на ребра, а V бројот на темиња во графот.
Да наведеме и неколку други можни примери. Најпрвин, забележете дека во алгоритамот погоре користевме цели броеви, но тежините на ребрата може да претставуваат и реални броеви – се додека тие се ненегативни. Единствените потребни промени во алгоритамот се во податочниот тип - vector<double> distance, priority_queue<pair<double, int> > pq, итн. Слично, имајте предвид дека, во нашиот пример, зборувавме за откривање на најкраток пат (во случајов, во километри) од едно почетно теме (извор) до останатите темиња. Кај други проблеми, може да се работи за најкраток пат во вид на поминати минути за патување од почетно теме до другите темиња. Алгоритамот, се разбира, нема никаков проблем со ова и истиот слободно може да се користи, бидејќи се работи за (практично) истиот проблем, само што тежините на ребрата ги дефинираме на друг начин (растојание во километри, потребни минути за патување, цена која што треба да се плати за патарина, итн).
Пред да продолжиме понатаму, многу е важно да се наведе и дека алгоритамот може едноставно да се промени за откривање и на точно кои темиња или ребра треба да се поминат во минималниот пат помеѓу изворот и некое друго теме (доколку, покрај растојанието кое што е запишано во distance[], сакаме да знаеме и низ точно кои темиња треба да поминеме). Имено, единствено нешто што треба да направиме е да креираме уште една низа (на пример, да ја наречеме истата parent[]), и онаму каде што вметнуваме нов елемент во приоритетниот ред (pq.push({ -distance[next], next }), да додадеме и parent[next] = city. Понатаму, ако на пример сакаме да го откриеме најкраткиот пат од изворот 0 до некој град Z, треба да видиме што е запишано во parent[Z] (нека таму е запишана вредноста Y, тоа е всушност градот кој треба да го поминеме пред Z), потоа да видиме што е запишано во parent[Y] (тоа е градот што треба да го поминеме пред Y), итн – нормално, се додека не дојдеме до делот каде што во parent[] имаме запишано 0 (темето кое го означува изворот, односно почетокот). Како што се движевме низ низата parent[], всушност ги откривме сите темиња кои што треба да се поминат на патот од изворот до соодветното теме: 0 -> ... -> X -> Y -> Z.
Минимално опфаќачко дрво
Во ова предавање ќе разгледаме уште еден класичен проблем – откривање на минимално опфаќачко дрво (minimum spanning tree). Ова ќе го направиме, пред се, бидејќи имплементацијата на алгоритамот за негово решавање е практично идентична со алгоритамот Dijkstra. Но, најпрвин, да објасниме што всушност е овој проблем. Накратко, да замислиме дека имаме податоци за некој неориентиран граф, неговите темиња и ребрата помеѓу нив. Опфаќачко дрво е дрво кое што ги содржи сите темиња од тој граф, но само дел од ребрата во графот кои се доволни за да сите темиња бидат поврзани помеѓу себе. На пример, ако имаме 3 темиња и ребра помеѓу темето 0 и темето 1, помеѓу темето 0 и темето 2 и помеѓу темето 1 и темето 2, можеме да избришеме едно од овие ребра и сите темиња повторно ќе бидат поврзани помеѓу себе (ќе постои пат од било кое теме до било кое друго – можеби поминувајќи низ трето теме). Минимално опфаќачко дрво е она опфаќачко дрво каде што збирот на тежините на ребрата е најмало можно.
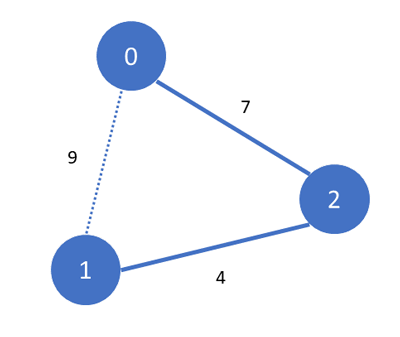
Со други зборови, да речеме дека имаме држава со неколку градови, и нека ни се познати растојанијата (во километри) помеѓу некои од нив - на пример, каде што може да се изградат патишта. Со користење на алгоритамот за откривање на минимално опфаќачко дрво, можеме да откриеме колку километри патишта треба да се изградат во државата, за да сите градови се поврзани меѓусебно. Со други зборови, минимално опфаќачко дрво претставува подмножество (дел) од ребрата на некој поголем неориентиран граф, така што сите темиња од тој граф се и понатаму поврзани меѓусебно (директно, или преку листа од ребра), и вкупниот збир на тежините на сите ребра во дрвото е најмала можна. Кажано поинаку, ако постојат повеќе начини да се извадат дел од ребрата на графот така што сите темиња во истиот ќе останат и понатаму меѓусебно поврзани, ние ќе ги извадиме оние ребра така што збирот на оние што ќе останат на крајот ќе биде најмал можен.
Имплементацијата на еден алгоритам за решавање на овој проблем (алгоритамот на Prim) е целосно идентична со имплементацијата на алгоритамот Dijkstra, со таа разлика што сега ќе сакаме да имаме една променлива која што ќе брои колку изнесува вкупниот збир на тежините на одбраните ребра (за да знаеме колку изнесува вкупната сума на ребрата во минималното опфаќачко дрво). Дополнително, кога ќе разгледуваме нов елемент за додавање во приоритетниот ред, како растојание до него наместо (distance[city] + distance_between_cities) ќе запишуваме само (distance_between_cities). Ова е логично – кај алгоритамот Dijkstra ни беше важно да го пресметаме вкупното растојание од изворот до теме, а во овој случај сакаме да го создаваме минималното опфаќачко дрво така што ќе правиме врски до другите темиња користејќи ги ребрата со најмала тежина (бидејќи сакаме да создадеме дрво каде што нивниот збир е најмал можен).
Дополнително, кај алгоритамот Dijkstra ни беше потребно да знаеме кое теме е изворот (т.е., од каде сакаме да ги разгледуваме растојанијата до останатите темиња), додека кај алгоритамот на Prim можеме слободно да одбереме било кое теме како почетно (бидејќи сите ќе создадат минимално опфаќачко дрво со потребниот најмал збир на тежини на ребрата). Она што го зборувавме е претставено со програмата дадена во продолжение:
Програма 17.2
//koristi C++11 - http://mendo.mk/Lecture.do?id=26
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int MAX_N = 101;
int N, E;
vector<pair<int, int> > G[MAX_N];
int prim(int start)
{
int sum = 0;
vector<int> distance;
distance.resize(MAX_N);
for (int i=0; i<MAX_N; i++)
{
distance[i] = 1000000000; //nekoj golem broj
}
priority_queue<pair<int, int> > pq;
distance[start] = 0;
pq.push({0, start});
int visited[MAX_N];
memset(visited, 0, sizeof(visited));
while (!pq.empty())
{
pair<int, int> state = pq.top();
pq.pop();
int city = state.second, distance_to_city = -state.first;
if (visited[city] == 0)
{
visited[city] = 1;
sum += distance[city];
for (auto edge : G[city])
{
int next = edge.first, distance_between_cities = edge.second;
if (distance[next] > distance_between_cities)
{
distance[next] = distance_between_cities;
pq.push({ -distance[next], next });
}
}
}
}
return sum;
}
int main()
{
cout << "Number of cities: " << endl;
cin >> N;
cout << "Number of edges: " << endl;
cin >> E;
cout << "Enter the edges (from, to, weight)." << endl;
for (int i=0; i<E; i++)
{
int from, to, weight;
cin >> from >> to >> weight;
G[from].push_back({to, weight});
G[to].push_back({from, weight}); //bidejki grafot e nenasocen
}
int start = 0; //pochnuvame od temeto 0
int sum = prim(start);
cout << "The minimum spanning tree has a sum of edges: " << sum << endl;
return 0;
}
Имплементацијата на алгоритамот Prim е навистина слична со имплементацијата на алгоритамот Dijkstra, па истиот едноставно се памети и е едноставен за разбирање. Кога ќе внесувате влезни податоци во програмата дадена погоре, внимавајте индексите на градовите да се од 0 до N-1, како и на тоа да постои ребро до секој град во графот кој го внесувате - со цел опфаќачкото дрво (одбирајќи ребра од оригиналниот граф) да може да состави пат до секое од темињата.
Покрај примерот со патната мрежа, да наведеме уште еден пример, за полесно да сфатиме какви проблеми се решаваат со пресметка на минимално опфаќачко дрво. Имено, да замислиме телекомуникациска компанија која што сака да постави кабли во некој град со вложување на најмалку можни средства (пари), така што сите згради ќе бидат поврзани. Во овој случај, ќе имаме почетен граф (од кој треба да одбереме дел од ребрата за минимално опфаќачко дрво) каде што темињата се зградите, а почетните ребра во графот ќе претставуваат кои згради може да се поврзат и колку изнесува цената за поставување на кабел помеѓу нив (која може да зависи од должината, дали кабелот ќе се постави над земја или подземно – со копање, итн). Во овој случај, минималното опфаќачко дрво ќе ја даде минималната цена така што сите згради ќе бидат поврзани во мрежата.
Забележете дека, за разлика од примерот прикажан погоре, алгоритамот Dijkstra решава комплетно различен проблем – откривање на растојание од едно теме до сите останати темиња. Кај тој алгоритам, целта е да се открие колку изнесува должината на најкраткиот пат од едно теме до едно или повеќе други темиња. Иако алгоритмите се слични во нивната имплементација, највеќе поради тоа што и двата користат приоритетен ред, тие сепак се користат за решавање на различни проблеми.




