Теоријата на графови се користи за решавање на разни проблеми. Како што ќе видиме во продолжение, кај голем дел од нив се среќаваат само два типа на објекти (претставени како темиња во графот). За ваквите графови, каде што темињата можат да се поделат на две множества и секое теме од едното множество може да се поврзе само со теме од другото множество, велиме дека се дводелни или бипартитни графови.

На пример, да замислиме граф со кој сакаме да претставиме работници (со едното множество) и работни места (со другото множество). Сега, ребрата можат да ги поврзуваат работните места со работниците кои се способни да ги пополнат истите - што значи дека ребрата ќе бидат помеѓу темиња од едното множество (работници) и темиња од другото множество (работни места). Нормално, нема да има ребра помеѓу работниците, или помеѓу работните места.

Во продолжение, ќе зборуваме за проблемот на пресметка на максимално спојување во дводелен граф (анг. maximum bipartite matching). Кај овој проблем, сакаме да одредиме колку најмногу ребра можат да се одберат од графот, така што секое од темињата е поврзано со најмногу едно ребро (не постојат две ребра кои завршуваат во исто теме). Доколку го искористиме проблемот со работниците и работните места кој го споменавме претходно, ова значи дека ќе има најмногу едно ребро кај секој работник и најмногу едно ребро кај секое работно место – односно, со користење на овој алгоритам, ќе пресметаме колку најмногу работни места можат да се пополнат, така што секој работник ќе работи најмногу една работа, и секое работно место ќе биде доделено на најмногу еден работник. Ова е исклучително корисен алгоритам, кој наоѓа примена во многу различни ситуации.

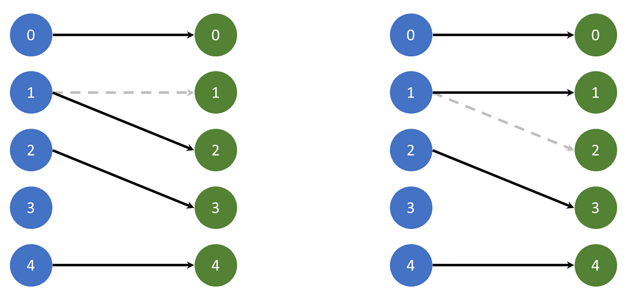
Како што можете да видите од сликите погоре, со црна боја се означени ребрата кои се дел од максималното спојување. Забележете дека и кај двете слики постои ребро од оригиналниот граф (работник кој е способен за одредено работно место) кое што не е дел од максималното спојување во дводелниот граф (означено со сива боја), бидејќи кај спојувањето не може повеќе ребра да завршуваат во исто теме. Во овој случај, со сликата сакаме да претставиме дека може да постојат повеќе начини да се изврши спојувањето, така што бројот на ребра ќе биде максимален (во овој случај, четири спојувања). Едноставно, доколку постојат повеќе начини, нашиот алгоритам ќе одбере еден од нив - бидејќи целта е да се направи максимално спојување (да пронајдеме работа за што е можно повеќе работници), и не е важно кои ребра ќе бидат одбрани од дводелниот граф.

Имплементација

Постојат повеќе алгоритми за решавање на овој проблем. Во продолжение, ние ќе го разгледаме оној кој што е наједноставен за имплементација, а сепак функционира исклучително ефикасно. За претставување на графот, како и во повеќето други алгоритми кои ги видовме досега, ќе користиме листи на соседство (кои, во овој случај, ќе ни ги означуваат почетните ребра – на пример, за проблемот со работниците, тоа е информацијата кој работник може да го пополни кое работно место).

Пред да ја видиме имплементацијата на овој алгоритам во програмскиот јазик C++, да споменеме накратко како истиот функционира. Главната идеја е обидот да се поврзе одредено теме од едното множество, разгледувајќи ги ребрата од истото, со било кое теме од другото множество. Доколку некое од темињата во другото множество е слободно (не е поврзано сеуште), тогаш ги означуваме овие две темиња (од едното и другото множество) како поврзани.

Доколку пак темето (нека го наречеме Y) од другото множество е веќе поврзано со некое теме X (од првото множество), тогаш рекурзивно ќе се обидеме да пронајдеме друга врска од X, со цел темето Y да ни се ослободи и да можеме истото да го искористиме. Со други зборови, со секој чекор се обидуваме да го зголемиме бројот на ребра (поврзувања) од едното до другото множество – притоа, ако е потребно, како во овој случај, некое ребро кое веќе сме го одбрале (X до Y) да го избришеме, тогаш тоа и ќе го направиме. Последното нешто на што треба да внимаваме е да имаме дополнителна низа seen[], која ќе ни означува кои темиња веќе сме ги разгледале, со цел рекурзијата да не заврши во бесконечен циклус на изминување на истите темиња и ребра.

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

const int MAX_N = 101;


//L go oznachuva brojot na elementi vo levoto mnozhestvo
//R go oznachuva brojot na elementi vo desnoto mnozhestvo
int L, R;
vector<int> G[MAX_N];

//left_of[i] oznachuva koj element od levoto mnozhestvo e
//povrzan so i-tiot element od desnoto mnozhestvo
//na primer, left_of[3] = 0 znachi deka elementot 3 od desnoto mnozhestvo
//e povrzan so elementot 0 od levoto mnozhestvo
int left_of[MAX_N];

//right_of[i] oznachuva koj element od desnoto mnozhestvo e
//povrzan so i-tiot element od levoto mnozhestvo
//na primer, right_of[0] = 3 znachi deka elementot 0 od levoto mnozhestvo
//e povrzan so elementot 3 od desnoto mnozhestvo
int right_of[MAX_N];


//pomoshna niza, koja se koristi za da znaeme koga da zapreme so rekurzijata
int seen[MAX_N];



//algoritamot pochnuva od funkcijata bipartite_matching(),
//pa zapochete i vie so chitanje od tamu
bool find_match(int index) 
{
     
     //index pokazhuva na elementi od levoto mnozhestvo
     if (seen[index]) 
     {
          return false;
     }
     
     seen[index] = 1;
     
     //obidi se da najdesh teme od desnoto mnozhestvo koe nema povrzuvanje
     for (int next : G[index]) 
     {
          if (left_of[next] == -1) 
          {
               //najdovme slobodno teme
               left_of[next] = index;
               right_of[index] = next;
               return true;
          }
     }
     
     //ne pronajdovme nishto, pa obidi se za premestish teme od desnoto mnozhestvo
     for (int next : G[index]) 
     {
          int current_connection = left_of[next];
          if (find_match(current_connection)) 
          {
               //ok, "next" e sega slobodno, povrzi go
               left_of[next] = index;
               right_of[index] = next;
               return true;
          }
     }
     
     
     //ne pronajdovme spojuvanje za "index"
     return false;
}


int bipartite_matching() 
{
     
     //koristime -1 za oznachuvanje deka ne postoi vrska
     memset(left_of, -1, sizeof(left_of));
     memset(right_of, -1, sizeof(right_of));
     
     int matched = 0;
     for (int i=0; i<L; i++) 
     {
          
          //postavi/resetiraj go "seen" so nuli
          //"seen" se koristi pri rekurzijata,
          //za da znaeme koga da zapreme
          memset(seen, 0, sizeof(seen));
          
          if (find_match(i)) 
          {
               matched++;
          }
     }
     
     return matched;
}




int main() 
{
     L = 5;
     R = 4;
     
     //napravi go pochetniot graf (na primer, koj rabotnik 
     //mozhe da raboti na koe rabotno mesto)
     //(indeksite pochnuvaat od 0)
     G[0].push_back(0);	//elementot 0 od prvoto mnozhestvo do 0 od vtoroto
     G[0].push_back(1);
     G[1].push_back(1);
     
     G[3].push_back(3);
     G[4].push_back(3);
     
     int matched = bipartite_matching();
     cout << "Matched " << matched << " elements." << endl;
     return 0;
}

Овој алгоритам е едноставен за имплементација, но истиот се користи многу често – пред се, бидејќи максималното спојување кај дводелен (бипартитен) граф има примена при решавањето на разни проблеми. Во продолжение, ќе споменеме неколку такви примери.

Слични примери

Во претходниот дел, веќе споменавме еден пример каде што може да се примени овој алгоритам – спојување на работници со потенцијални работни места. Дополнително, се разбира, истиот може да се примени и на други варијации од истиот проблем – на пример, спојување на ментори со ученици (каде ребрата означуваат кој ментор може да му помогне на ученик во соодветната област – на пример, ментор по математика со ученици кои имаат проблем по тој предмет).

Покрај ова, можно е да постојат и проблеми каде што треба да направиме мала анализа пред да го создадеме графот, а потоа и само да го повикаме алгоритамот кој го видовме погоре. На пример, да замислиме дека во некој град има проблем со пронаоѓање на паркинг места, и одлучиме да направиме дводелен граф каде што од едната страна на графот ќе претставиме множество од коли, а од другата страна ќе претставиме множество од паркинг места. Сега, да речеме дека од нас се бара да пресметаме на колку најмногу коли може да им се доделат паркинг места, доколку луѓето не сакаат да ја паркираат нивната кола подалеку од 3 километри од местото во кое живеат?

Во овој случај, веќе ни е дадено множеството на коли и множеството на паркинг места, и ние само треба да ги создадеме почетните ребра во дводелниот граф (коли до потенцијални паркинг места). Па, единствено што треба да направиме е од секоја кола (која припаѓа на некој жител), да направиме ребра до паркинг местата кои се на оддалеченост од најмногу 3 километри од местото каде живее сопственикот на таа кола. Понатаму, овој граф ни е веќе комплетен (ги знаеме темињата и листите на соседство), па само треба да го извршиме алгоритамот прикажан погоре.

Да разгледаме сега уште еден проблем. Нека имаме неколку коцки (коцките имаат 6 страни), на кои е запишана по една цифра (0 до 9) на секоја страна од коцките. На пример, може да имаме коцка на која се запишани цифрите 1, 3, 5, 3, 0, 4 – по една цифра на секоја страна од коцката. Сега, што ако треба да пресметаме дали дел од овие коцки може да се наредат една по друга, така што на нив ќе биде испишан одреден број (на пример, 59391401), како што е прикажано на сликата? Дали можеме да напишеме програма за решавање на овој проблем?

И овој пример може да се реши со помош на алгоритамот за пресметка на максимално спојување во дводелен граф. Единствено што треба да направиме е да ги ставиме коцките како едно множество во графот (секоја коцка е едно теме), а секоја од цифрите во бројот кој треба да го создадеме ќе биде дел од другото множество во дводелниот граф. Понатаму, ќе ги поврземе темињата (со ребра), така што коцка (една страна на графот) ќе поврземе со цифра (друга страна на графот), доколку коцката ја има таа цифра на едната од шесте свои страни. По извршување на алгоритамот, треба само да провериме колку поврзувања успеал истиот да направи. Доколку сме успеале да ги поврземе сите цифри од бројот со некоја коцка, тогаш сме го решиле оригиналниот проблем – во спротивно, не е можно со коцките кои ги имаме на располагање да го решиме истиот.

Забележете дека, кај овој проблем, користевме ваков алгоритам бидејќи секоја коцка може да се искористи само еднаш (за запишување на само една цифра од бројот). Доколку ова не беше случај, само ќе проверевме (со некој едноставен алгоритам) дали постои секоја од цифрите кај било која коцка. За полесно да го разберете ова, замислете коцка каде што на сите шест страни се наоѓа цифрата 1, и друга коцка каде што на сите шест страни се наоѓа цифрата 2. Сега, ако треба со помош на овие коцки да го запишеме бројот "11", тоа не можеме да го направиме - бидејќи ако ја искористиме првата коцка за пишување на првата цифра од "11", тогаш веќе немаме друга коцка (на која имаме страна со цифра 1) за да ја запишеме и втората цифра од "11".

Имплементацијата на оваа програма е дадена во продолжение, со влезни податоци кои се состојат од 5 коцки и бројот “2304” (се разбира, истите може да се променат). Забележете дека алгоритамот за откривање на максимално спојување е (нормално) ист како и претходно, па тука само е дадено како изгледа функцијата main().

//koristi C++11 - http://mendo.mk/Lecture.do?id=26

int main() 
{
     vector<string> dice;
     dice.push_back("135420"); //kocka so strani 1, 3, 5, 4, 2, 0
     dice.push_back("111222"); //kocka so strani 1, 1, 1, 2, 2, 2
     dice.push_back("353535"); //kocka so strani 3, 5, 3, 5, 3, 5
     dice.push_back("038905"); //kocka so strani 0, 3, 8, 9, 0, 5
     dice.push_back("888888"); //kocka so strani 8, 8, 8, 8, 8, 8
     
     string number = "2304";
     L = dice.size();
     R = number.size();
     
     //sozdadi gi rebrata vo grafot
     for (int i=0; i < dice.size(); i++) 
     {
          for (int d=0; d < number.size(); d++) 
          {
               
               char digit_on_number = number[d];
               bool edge_from_dice_to_digit = false;
               
               //ako kockata ja ima cifrata, kje napravime rebro pomegju niv
               for (auto digit_on_dice : dice[i]) 
               {
                    if (digit_on_dice == digit_on_number) 
                    {
                         edge_from_dice_to_digit = true;
                    }
               }
               
               
               if (edge_from_dice_to_digit)
               {
                    G[i].push_back(d);
               }
          }
     }
     
     int matched = bipartite_matching();
     if (matched == number.size()) 
     {
          cout << "Wohoo. Successfully wrote all digits of the number." << endl;
     }
     return 0;
}

Во ова предавање, се запознавме со проблемот на спојување на темиња во дводелен (бипартитен) граф, како и со алгоритамот за откривање на максимално спојување. Вакви задачи се среќаваат во многу различни форми (како при работа на разни проблеми во реалниот живот, така и за време на натпревари), па имајте го алгоритамот во предвид кога разгледувате некој проблем каде што се бара откривање на врски помеѓу два типа на објекти, кога се бара кој е најдобриот начин да се поврзат елементи со цел оптимално доделување на работа или задолженија, итн.

Дозвола за користење: CC BY-NC 2.5 ©