Принцип на вклучување и исклучување
При пишувањето на програми и разни софтверски решенија, често се среќаваме со ситуации каде што треба да изброиме предмети или објекти кои задоволуваат одреден услов. Најчесто, ова го правиме преку директна пресметка на бараниот број. Но, постојат ситуации кога всушност е полесно да се пристапи кон пресметка на бројот на предмети или објекти кои не го задоволуваат бараниот услов, и тој број да го одземеме од вкупниот број на предмети или објекти. На пример, доколку треба да пресметаме колку лица во Република Македонија се моментно на слобода, можеме да одлучиме дека е подобро да го откриеме бројот на лица кои се моментно во затвор, и тој број да го одземеме од бројот на жители според последниот попис. Ова го правиме бидејќи бројот на затвореници е полесен за пресметка – истиот е многу помал, и треба само да имаме информација колку затвореници има во секоја установа за отслужување на казна.
Покрај ова, постојат и проблеми каде што треба да решиме многу покомплицирани ситуации – имено, ако постојат повеќе множества на објекти или можни вредности, и ние треба да ги искористиме истите за да решиме некој поголем проблем. На пример, што доколку треба да пресметаме колку броеви помали од 100 се деливи со 3 или се деливи со 5? Еден алгоритам кој можеме да го примениме е да ги испробаме сите броеви од 1 до 100, во однос на тоа колку од нив се деливи или со 3 или со 5. Во овој случај, постојат 47 броеви кои се деливи или со 3 или со 5.
Многу поефикасен начин (со кој што можеме да решаваме вакви и слични проблеми за многу поголеми броеви од 100), е преку користење на т.н. принцип на вклучување и исклучување. Поконкретно, принципот на вклучување и исклучување е техника на броење која што претставува генерализација (проширување) на основната идеја за одредување на број на елементи во унија на две множества - имено, дека бројот на елементи во таа унија е еднаков на: збирот од бројот на елементи во првото множество и бројот на елементи во второто множество, минус бројот на елементи во нивниот пресек, како што е прикажано на сликата подолу.
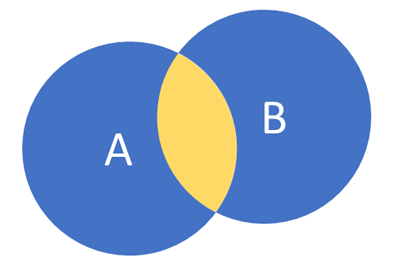
Во однос на проблемот кој го видовме претходно, ова би значело дека можеме да откриеме колку броеви се деливи со 3 или со 5, доколку пресметаме колку броеви се деливи само со 3 (тоа е лесно, бидејќи бројот е еднаков на 100/3=33, доколку не го земеме во предвид остатокот од делењето), понатаму колку броеви се деливи само со 5 (100/5=20), и од нивниот збир (33+20=53), го одземеме бројот на елементи кои се деливи и со двата броја (тоа се всушност броевите деливи со 3*5=15, па имаме 100/15=6). Значи, резултатот би бил еднаков на 53-6=47.
Принципот на вклучување и исклучување овозможува решавање на вакви проблеми и кога имаме повеќе од 2 можни множества - па, на пример, за да го пресметаме бројот на елементи во унија на 3 множества (нека ги именуваме A, B и C), треба да ги собереме сите овие вредности (внимавајте на знакот, + за собирање, и - за одземање):
| знак | вредност |
|---|---|
| + | бројот на елементи во првото множество |
| + | бројот на елементи во второто множество |
| + | бројот на елементи во третото множество |
| - | бројот на елементи во пресекот на првото и второто множество |
| - | бројот на елементи во пресекот на првото и третото множество |
| - | бројот на елементи во пресекот на второто и третото множество |
| + | бројот на елементи во пресекот на првото, второто и третото множество |
Сликовито, ова можете да го забележите и од сликата дадена подолу.
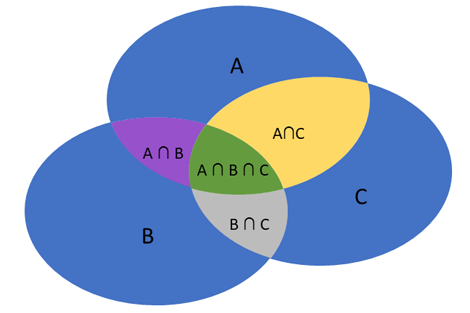
Во овој момент, доколку не успеавте да забележите од двата примери, треба да споменеме дека е всушност многу едноставно да се открие кој знак (+ или -) треба да стои пред секоја група. Имено, ако во групата имаме непарен број на множества (еден, три, пет, итн), тогаш пред групата стои знакот +, а доколку имаме парен број (два, четири, итн), тогаш стои знакот -. Поради тоа, ако видите погоре, имаме знак “-” и го одземаме “бројот на елементи во пресекот на првото и второто множество” (бидејќи има пресек од две множества). Од друга страна пак, имаме знак “+” и го додаваме “бројот на елементи во пресекот на првото, второто и третото множество”.
Во првиот пример што го видовме со делењето со 3 и 5, најпрвин ги собравме броевите (100/3) и (100/5), бидејќи разгледувавме по едно множество (едното е “делив со 3”, а другото “делив со 5”), а потоа од тој збир го одземавме бројот (100/15), бидејќи таму разгледувавме пресек од две множества (“делив со 3" и "делив со 5”).
Забележете дека ваков начин на пресметка на тоа колку броеви во првите 100 се деливи и со еден број (X) и со друг број (Y) преку делење на 100 со нивниот производ (X*Y), може да се врши само доколку и двата броја се (заемно) прости, што во овој случај е точно. Доколку не е точно, тогаш треба да пронајдеме друг начин за пресметка на бројот на елементи во пресекот на множествата. Принципот на вклучување и исклучување единствено ја прикажува поврзаноста на унијата на било кои множества со нив и нивните пресеци, а пресметката колку броеви се наоѓаат во пресекот е оставена на вас. Во конкретниот случај, едноставно е да се пресмета бројот на елементи во пресекот доколку имаме прости делители, па затоа го искористивме тој пример.
Подмножества
Во претходниот дел, зборувавме за тоа како да откриеме кој знак стои пред секоја група. Но, како всушност, со користење на компјутер, можеме да ги создадеме сите овие групи од по 1 множество, па 2 множества (за нив да ги одземеме), па 3 множества (за да ги додадеме), итн? Одговорот е многу едноставен – во овој случај, ние всушност ги разгледуваме сите можни подмножества на листата од множества која ни е дадена на почеток. На пример, доколку имаме 2 множества (A и B), тогаш подмножества на оваа листа се: {} (празното подмножество не не интересира, па го игнорираме), {A}, {B}, {A, B}. Доколку имаме 3 множества (A, B, и C), тогаш подмножества на оваа листа се: {} (го игнорираме), {A}, {B}, {C}, {A, B}, {A, C}, {B, C}, {A, B, C}.
Се разбира, веќе знаеме и кој знак (+ или -) ќе стои пред секое од нив, имајќи во предвид дека е лесно да се утврди бројот на елементи во едно подмножество: 1 за {C}, 2 за {B, C}, 3 за {A, B, C}, итн.
Имајте во предвид дека во ова предавање зборуваме за принципот на вклучување (+) и исклучување (-), и веќе споменавме дека е потребно да ги создадеме сите можни подмножества од некоја листа (на пример, A, B, C). Сега, време е да се потсетиме како воопшто можат истите (едноставно) да се идентификуваат со помош на компјутер. Всушност, ова е проблем за кој веќе зборувавме во едно од претходните предавања, и наједноставниот начин за решавање на истиот е преку разгледување на битовите на еден цел број. Имено, доколку имаме листа од N елементи (A, B, C, D, …), тогаш постојат 2N подмножества од оваа листа.
Сега, доколку знаеме дека постојат 2N подмножества, можеме да искористиме еден for циклус кој ќе ги измине сите цели броеви од 0 до 2N -1, и тие броеви (запишани бинарно) изгледаат вака (во случајов, ќе користиме пример каде N=3):
| бинарно | декадно | множество |
|---|---|---|
| 000 | (0) | [] |
| 001 | (1) | [A] |
| 010 | (2) | [B] |
| 011 | (3) | [A, B] |
| 100 | (4) | [C] |
| 101 | (5) | [A, C] |
| 110 | (6) | [B, C] |
| 111 | (7) | [A, B, C] |
Нека кажеме дека оној бит (0 или 1) кој се наоѓа најдесно во секој од броевите ќе означува дали A е дел од тоа подмножество, нека оној бит (0 или 1) кој се наоѓа втор од десно означува дали B е дел од тоа подмножество, итн. Така, на пример, 001 соодветствува на подмножеството [A], бидејќи само последниот бит е еднаков на 1. Слично, 111 соодветствува на [A, B, C] бидејќи сите битови се еднакви на 1, итн. Инаку, најчесто, секој од N-те елементи во листата (A, B, C, D, ...) го заменуваме со некој од броевите од 0 до N-1 за полесно користење од страна на компјутерите, па разгледуваме листа (0, 1, 2, 3, … N-1).
Следната програма ќе ги отпечати сите подмножества (A, B, C, D, итн), за даден број на елементи N.
Програма 22.1
#include <iostream>
#include <string>
using namespace std;
int main()
{
int N;
cin >> N;
//(1 << N) e ednakvo na 2^N
for (int i=0; i < (1 << N); i++)
{
string current = "";
for (int j=0; j < N; j++)
{
//proveri dali j-tiot bit (gledano od pozadi) e 1
if (((1 << j) & i) != 0)
{
char ch = ('A' + j);
current += ch;
}
}
//otpechati go tekovnoto podmnozhestvo
cout << current << endl;
}
return 0;
}
Ако сеуште не ви е јасно како функционира оваа програма, посетете го продавањето за битови, каде што овој алгоритам е објаснет многу подетално. Единствено што ќе споменеме во овој дел е дека со условот ((1 << j) & i) != 0), проверуваме дали ј-тиот бит (гледано од десно налево) во бројот i е еднаков на 1. Имено, со (1 << j) добиваме број кој што има само еден бит (оној на j-тата позиција) со вредност 1, а потоа со помош на операторот AND (&) проверуваме (бит по бит) кои битови и во двата броја се еднакви на 1. Бидејќи постои само еден бит во бројот (1 << j) кој е еднаков на 1, тогаш оваа вредност ќе биде различна од 0 само кога и битот на истата позиција во бројот претставен со променливата i ќе биде еднаков на 1.
Пример
Во претходниот дел, зборувавме дека принципот на вклучување и исклучување се базира на идејата дека некои проблеми каде што треба да пресметаме број на елементи во унија од множества може да се решат користејќи го бројот на елементи во самите множества и бројот на елементи во нивните пресеци. Зборувавме како да ги создадеме сите подмножества (кои ни се потребни со цел да знаеме од кои множества да бараме пресек), и како да знаеме дали едно подмножество ќе влијае позитивно на бројот (вклучување, со +), или ќе влијае негативно на бројот (исклучување, со -).
Всушност, со тоа комплетно сме ја објасниле идејата и начинот на кој можеме да го користиме овој принцип. Дополнително, веќе видовме и пример каде што со истиот може да се пресмета колку броеви се деливи со еден или повеќе прости броеви (3, 5, итн).
Во овој дел, ќе се обидеме да разгледаме уште еден пример (многу посложен од претходно), со цел подобро да разбереме за што се работи. Не грижете се доколку не го разберете решението веднаш.
Да го објасниме проблемот кој сакаме да го решиме. Имено, нека имаме два броја N и M, и нека треба да пресметаме колку броеви помали или еднакви на N немаат заеднички делител со бројот M. Притоа, 1 не се важи како делител, бидејќи во тој случај задачата ќе нема смисла (сите броеви се деливи со 1).
На пример, ако N=20 и M=6, нашата програма треба да отпечати 7, бидејќи постојат 7 броеви помали или еднакви на 20, кои немаат заеднички делител со 6 - тоа се: 1, 5, 7, 11, 13, 17, 19. Забележете дека, на пример, 8 не е во оваа листа бидејќи 2 е заеднички делител на 8 и М=6; понатаму 9 не е во оваа листа бидејќи 3 е заеднички делител на 9 и M=6, итн.
Оваа задача можеме да ја решиме со помош на принципот на вклучување и исклучување. Притоа, идејата што треба да ја користиме за нејзино решавање произлегува од примерот даден претходно (каде елиминиравме одредени броеви како 8 и 9, со прости броеви кои се делители и на тие броеви и на M: 2 и 3). Доколку елиминираме одредени броеви како такви кои имаат заеднички делител со M, тогаш конечниот резултат ќе биде еднаков на N минус бројот на такви броеви. Поконкретно, ако N=20 и постојат 13 броеви кои имаат заеднички делител со M=6, тогаш имаме 20-13=7 броеви кои немаат заеднички делител. (Доколку ова не ви е јасно, погледнете во првите реченици од ова предавање.)
Понатаму, за да елиминираме некој број како таков кој има заеднички делител со M, доволно е да пронајдеме само еден број кој е делител и на него и на бројот M. Притоа, најдобар избор е да ги гледаме простите делители на бројот, бидејќи секој број поголем од 1 може да се претстави преку производ на неговите прости делители.
Од кога го знаеме ова, можеме да го искористиме истиот алгоритам кој го користевме и претходно. Имено, нека ги разгледуваме повторно броевите N=20 и M=6. Доколку го претставиме бројот M=6 преку неговите прости делители, ќе видиме дека тие се 2 и 3. Сега, потребно е само да одредиме колку броеви помали или еднакви на N се деливи со 2, колку се деливи со 3, и колку се деливи со 2*3. Во овој случај, имаме 20/2=10 броеви деливи со 2, имаме 20/3=6 броеви деливи со 3, и имаме 20/6=3 броеви деливи и со 2 и со 3. Според принципот за кој зборувавме претходно (подмножествата со непарен број на елементи се земаат со знак +, а оние со парен број на елементи со знак -), ги вклучуваме (со знак +) вредностите 10 и 6, а ја исклучуваме (со знак -) вредноста 3. За бројот 3 искористивме знак минус (исклучување), бидејќи тој произлегува од пресметката 20/6=3, односно тоа е “бројот на елементи кои се деливи со 2 и деливи со 3”, односно тоа е пресек на две множества (”делив со 2” и ”делив со 3”), па бидејќи имаме парен број на елементи, ќе имаме и исклучување. Конечната пресметка е 10+6-3 = 13, односно дека имаме 13 броеви кои имаат заеднички делител со M. Според ова, постојат 20-13=7 броеви кои немаат заеднички делител со M.
Реализацијата на оваа идеја за било кои броеви N и M, имплементирана во програмскиот јазик C++, е дадена во продолжение.
Програма 22.2
#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> find_prime_divisors(int N)
{
vector<int> divisors;
//se dvizhime do kvadratniot koren na N (i <= sqrt(N)) = (i*i <= N)
//bidejki ako ima delitel pogolem od sqrt(N),
//togash postoi i pomal delitel, pa toj kje go najdeme prvo
for (int i=2; i*i <= N; i++)
{
if ((N%i) == 0)
{
divisors.push_back(i);
//najdovme delitel, nema potreba da go dodavame istiot povekje pati
while ((N%i) == 0)
{
N /= i;
}
}
}
//mozhebi prost broj ostanal vo N, ili N bil prost broj na pochetokot?
if (N >= 2)
{
divisors.push_back(N);
}
return divisors;
}
//brojot na elementi vo edno mnozhestvo mozhe da se presmeta
//kako brojot na bitovi ednakvi na 1
int elements_in_subset(int subset)
{
int one_bits = 0;
//izminuvaj go brojot bit po bit...
//delenjeto so 2 go brishe posledniot bit
while (subset > 0)
{
if ((subset % 2) == 1)
{
one_bits++;
}
subset /= 2;
}
return one_bits;
}
int calculate(int N, int M)
{
vector<int> divisors = find_prime_divisors(M);
int divisors_count = divisors.size();
int bad_numbers_count = 0;
//gi razgleduvame site podmnozhestva - takvi postojat 2^(divisors_count)
//pochnuvame od i=1, bidejki ne ne interesira praznoto podmnozhestvo [].
for (int i=1; i < (1 << divisors_count); i++)
{
int product = 1; //proizvod na elementite vo podmnozhestvoto
//za da znaeme kolku da dodademe ili odzememe.
//na primer, za "deliv so 2" i "deliv so 3", imame product=2*3
for (int j=0; j < divisors_count; j++)
{
if ((i & (1 << j)) != 0)
{
//vo proizvodot vleguvaat onie vrednosti koi se del
//od podmnozhestvoto definirano so "i"
product *= divisors[j];
}
}
//kolku vrednosti ima vo presekot, na primer
//ako N=20, togash ima 20/6=3 broevi delivi i so 2 i so 3.
int number_of_values = (N / product);
if ((elements_in_subset(i) % 2) == 1)
{
//ako ima neparen broj na elementi, dodavame
bad_numbers_count += number_of_values;
}
else
{
//ako ima paren broj na elementi, odzemame
bad_numbers_count -= number_of_values;
}
}
return (N - bad_numbers_count);
}
int main()
{
int N, M;
cin >> N >> M;
cout << calculate(N, M) << endl;
return 0;
}
Иако примерот кој го решивме со претходната програма е поприлично сложен, сепак тој е одличен проблем за разгледување, бидејќи скоро сите проблеми кои можат да се решат со помош на принципот на вклучување и исклучување се базираат на иста или слична идеја. На пример, истиот беше солидна можност да се потсетиме како може да разгледуваме подмножества со помош на едноставна игра со битови. Со други зборови, лесно можеме да ги создадеме сите подмножества, а и едноставно е да се утврди бројот на елементи во нив преку разгледување на бројот на битови. Слично, доколку за некој проблем можеме едноставно да смислиме како да го пресметаме бројот на елементи во пресекот на множествата кои се дефинирани со истиот, тогаш можеме тие броеви едноставно да ги собереме (вклучиме) или одземеме (исклучиме), со цел да ја пресметаме бараната вредност за бројот на елементи во нивната унија.




