Given are n rectangles, numbered from 1 to n. We place them tightly on the axis OX, from left to right, according to rectangles’ numbers. Each rectangle stays on the axis OX either by its shorter or by its longer side (see the picture below). Compute the length of the upper envelop line, i.e. perimeter’s length of the obtained figure minus the length of the left, right and bottom straight line segments of the picture.

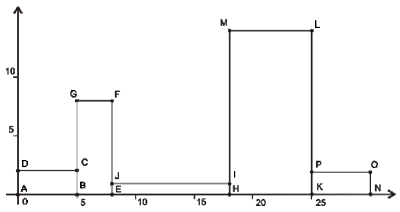Write program rec to find the maximum possible length of the upper envelop line.

Input

On the first line of the standard input, the value of n is written. On each of the next n lines, two integers are given – a_i and b_i – the side lengths of the i-th rectangle.

Constraints: 0 < n < 1000; 0 < a_i < b_i < 1000, for each i = 1, 2, ..., n.

Output

On a line of the standard output, your program should write the result as a positive integer.

Constraints

Time limit: 1 second
Memory limit: 64 megabytes

Examples

input
5
2 5
3 8
1 10
7 14
2 5

output
68

Explanation: A configuration, that yields the maximum length of the upper envelop line, is presented on the picture.

The upper envelop line consists of segments DC, CG, GF, FJ, JI, IM, ML, LP, and PO. The total length is 5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 + 5 = 68.