Emil is preparing for a competition in Summing, a game involving N special tiles with numerical values written on them. The objective of the game is to take tiles and sum their values to get as close as possible to a target number without exceeding it.

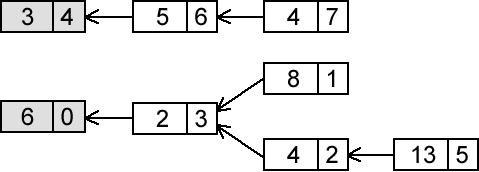Each tile is marked with a unique integer ID, a value and a number that determines its "predecessor". During a game, a tile may only be taken directly after its predecessor. Some of the tiles are called "starting tiles" (marked by a predecessor ID of -1) and these are the only tiles that may be taken at the start of a game. Exactly one starting tile may be taken during a game.

In other words, you play the game of Summing by first taking a tile with a predecessor ID of -1, then a tile whose predecessor is the tile you took in step 1, then a tile whose predecessor is the tile you took in step 2, etc. After you take at least one tile, you can stop at any time. Please note that, in the image above, starting tiles are marked with grey color and there are arrows pointing from tiles to their predecessors. Note that the ID is written on the right side of the tile, while the value is written on the left side.

Emil wants you to help him prepare for the tournament and write a program that can play Summing. Your program should be able to read several different target numbers, and output the best sum for each of those numbers. Each target number represents a new game.

Input

The first line of input contains two integers N (1 ≤ N ≤ 100000) and Q (1 ≤ Q ≤ 100000) - the number of different tiles and the number of target numbers for which your program has to find the best sum.

Each of the following N lines describes a single tile in the format "Vi Pi", where Vi (0 ≤ Vi ≤ 20000) is the value of the tile and Pi is the ID of its predecessor. The tile with ID number i is described in the i-th of those lines (0-based). There will be at least one tile with a predecessor ID of -1. No tile will have itself as a predecessor.

Each of the following Q lines contains one integer Ti (1 ≤ Ti ≤ 2000000000) - the i-th target number.

In test cases worth 20% of the full score, there will be exactly 1 starting tile, each tile will be reachable from the starting tile through a series of tiles and no two tiles will have the same predecessor.

Output

Your program should output the best sum for each target number (in the same order that the target numbers were given in the input). If no reachable sum is less than or equal to the target number, print "none" (quotes for clarity).

Constraints

Time limit: 1 second
Memory limit: 64 megabytes

Examples

input
8 5
6 -1
8 3
4 3
2 0
3 -1
13 2
5 4
4 6
4
8
9
20
2

output
3
8
8
16
none