This year, Ohrid will host an international mountain running competition. Since runners need a lot of water to sustain them, the organizers have prepared a set of locations where refreshment stations may be set up, and have connected them in a large directed cycle via one-directional trails (as shown on the image below). The refreshment stations are named S₀ to S_N-1 (going along the direction of the cycle), and the trail T_i connects stations S_i and S_i+1 (directed toward S_i+1) - where S_N = S₀.

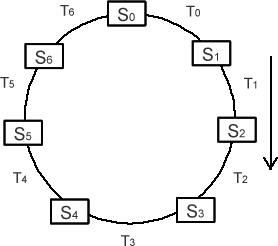It is known that a runner will spend exactly K_i units of water to finish trail T_i, and each runner will be able to get at most W_i units of water at refreshment station S_i. There is no limit to the amount of water a runner may carry at any time, but the time in minutes a runner needs to finish a trail is equal to the number of units of water he started the trail with - so if a runner starts trail T₁ with 5 units of water, then he will finish it in 5 minutes regardless of the amount of water he spends on the trail.

The organizers are now considering possible start and end points for the race (the race must start from and finish at a refreshment station). They want you to write a program that, for each of the Q pairs of start and end refreshment stations given to it, will calculate and output the minimum time necessary for an optimal runner to finish the given race. Note that the runner may start the race with at most as much water as is available at the starting refreshment station.

Input

The first line of input contains two integers N (3 ≤ N ≤ 1000) and Q (1 ≤ Q ≤ 100000) - the number of trails, and the number of pairs of start and end refreshment stations that the organizers are considering.

The second line of input contains N integers W_i (1 ≤ W_i ≤ 1000000) - the units of water available at each refreshment station (starting with station S₀).

The third line of input contains N integers K_i (1 ≤ K_i ≤ 1000000) - the units of water required to finish each trail (starting with trail T₀).

Each of the following Q lines contains two distinct integers Si and Ei (0 ≤ S_i, E_i ≤ N-1) - the pairs for starting and ending refreshment stations.

In test cases worth at least 40% of the full score, the number of refreshment stations will be at most 100 (3 ≤ N ≤ 100) and all W_i and K_i will be at most 10 (1 ≤ W_i, K_i ≤ 10).

Output

For each pair of starting and ending locations, in the same order as they are given in the input, your program should output the minimum time necessary for an optimal runner to finish the given race. If the race cannot be completed, your program should output "-1" (quotes for clarity).

Constraints

Time limit: 1 second
Memory limit: 64 megabytes

Examples

input
7 4
3 2 5 2 5 1 6
2 4 3 1 6 1 2
0 1
4 5
2 5
5 1

output
2
-1
11
5