Train
A railway company just launched a new train prototype made out of a single railway wagon
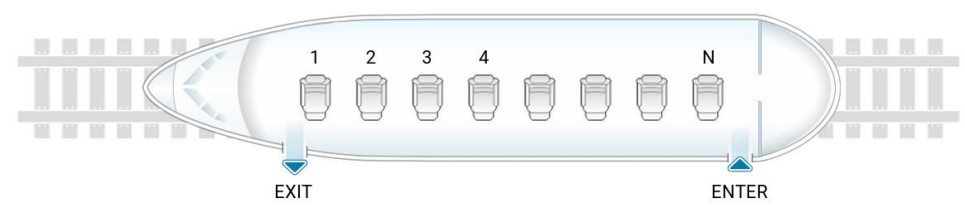
containing N chairs. Each chair is labelled from 1 to N (starting at the front of the train) and they
are arranged in a row, one behind the other. The following rules must be followed by every
passenger:
1. Passengers must board the train only through the rear door which is located behind all seats. Once inside the train, passengers are only allowed to move towards the front of the cabin
and may exit the train only through the front door (located in front of all seats).
2. Each passenger must take the seat immediately behind the last occupied chair. If the train is fully empty, the passenger must take the front seat (labeled as seat 1).
3. No passenger is allowed to leave their seat until disembarkment.
4. At each train station, passengers that have reached their destination will exit the train. If there are passengers that are seated in front of a passenger that has reached his destination,
they must also exit the train even if they have not reached their destination.
5. Once a passenger exits the train, they will not be allowed to reboard.
 |
Train route contains M stations, each labelled from 1 to M. The train will stop at each station,
starting with station 1 and ending with station M. Across all M train platforms, there are a total of N
passengers, labelled from 1 to N. The ticket price, as well as the boarding and destination stations
are known in advance for each passenger.
The railway company wants to have only happy customers that reach their destination. In order to
have only happy customers, the company allowed the conductor to choose which passengers can
board and in which order they are allowed to do it. So, the conductor can choose to not allow
certain passengers to board.
Find out what is the largest profit that the company can make having only happy customers, and
also one valid ordering of embarkment that would yield this profit.
Input
The input contains the following:
1. the first line lists the pair of numbers N (1 ≤ N ≤ 100000) and M (1 ≤ M ≤ 2·109)
2. the following N lines list the travel requirement for each passenger x y c (1 ≤ x < y ≤ M, 1 ≤ c ≤ 10000), such that x represents the boarding station, y represents the destination station and c is the ticket price.
Within each line, the numbers are positive integers and are separated by exactly one space.
Output
The output should have the following format:
1. the first line should contain a number P representing the maximum amount of money that
the railway company can make;
2. the second line should contain a number Num representing the number of passengers that
were able to reach their destination in an optimal solution, i.e. with the largest profit;
3. the third line should contain the labels for each passenger that reached their destination, in
boarding order, in this optimal solution. All passenger labels must be separated by exactly
one space.
Any passenger configuration that provides the maximum profit for the company will be considered correct.
Constraints
Time limit: 1 second
Memory limit: 128 megabytes
Examples
input 4 8 2 6 10 4 5 1 3 7 10 1 7 10 | output 20 2 1 3 |
input 4 10 1 3 3 1 10 2 2 5 3 1 2 5 | output 11 3 4 1 3 |
Explanation for the first test:
A correct answer can be obtained as such:
station 2: passenger 1 boards the train
station 3: passenger 3 boards the train
station 6: passenger 1 exits the train
station 7: passenger 3 exits the train
Explanation for the second test:
A correct answer can be obtained as such:
station 1: passengers 4 and 1 board the train
station 2: passenger 4 exits the train and passenger 3 boards the train
station 3: passenger 1 exits the train
station 5: passenger 3 exits the train




